Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
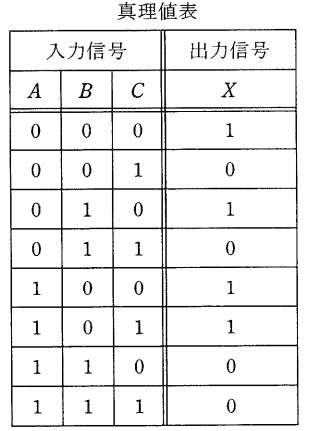
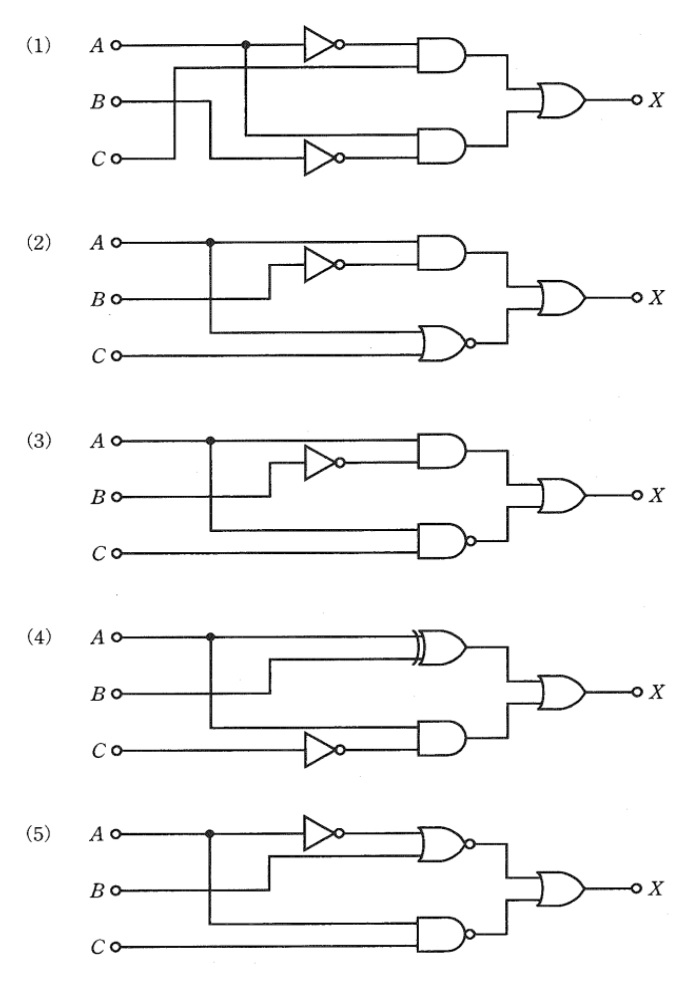
入力信号が\( \ A \ \),\( \ B \ \)及び\( \ C \ \),出力信号が\( \ X \ \)の論理回路として,次の真理値表を満たす論理回路は次のうちどれか。
【ワンポイント解説】
真理値表から,適当な論理回路を選択する問題です。
真理値表の全てのパターンを入れていると時間がなくなってしまうので,順番に\( \ 2 \ \)つか\( \ 3 \ \)つ程度の信号を入れて選択肢を絞っていくのが最も効率的な方法かと思います。
1.主な論理回路の真理値表
基本的な論理回路と図記号は覚える必要がありますので,以下の真理値表を覚えておきましょう。
①\( \ \mathrm {AND} \ \)回路
論理積といい,すべての入力が\( \ 1 \ \)の時のみ\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 1 \\
\end{array}
\]

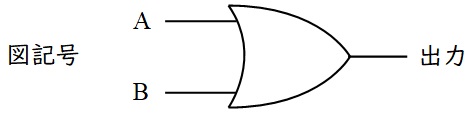
②\( \ \mathrm {OR} \ \)回路
論理和といい,入力が一つでも\( \ 1 \ \)の時\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{array}
\]
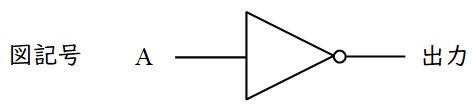
③\( \ \mathrm {NOT} \ \)回路
論理否定といい,入力を反転する回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{c|c}
\mathrm {A} & 出力 \\
\hline
0 & 1 \\
1 & 0 \\
\end{array}
\]
④\( \ \mathrm {NAND} \ \)回路
\( \ \mathrm {NOT}+\mathrm {AND} \ \)で\( \ \mathrm {AND} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわちすべての入力が\( \ 1 \ \)の時のみ\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
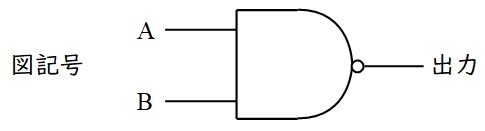
⑤\( \ \mathrm {NOR} \ \)回路
\( \ \mathrm {NOT}+\mathrm {OR} \ \)で\( \ \mathrm {OR} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわち入力が一つでも\( \ 1 \ \)の時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 0 \\
\end{array}
\]
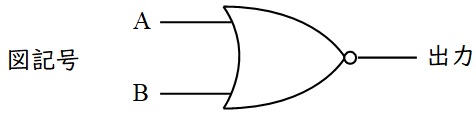
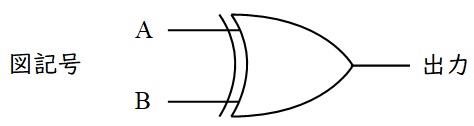
⑥\( \ \mathrm {ExOR} \ \)回路
排他的論理和\( \ \left( \mathrm {exclusive \ or} \right) \ \)といい,入力が異なるとき\( \ 1 \ \),入力が同じ時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
【解答】
解答:(2)
解答の各論理回路に\( \ A=0 \ \),\( \ B=0 \ \)及び\( \ C=0 \ \)を入力すると図1のようになり,出力\( \ X=1 \ \)となるのは(2),(3),(5)となる。
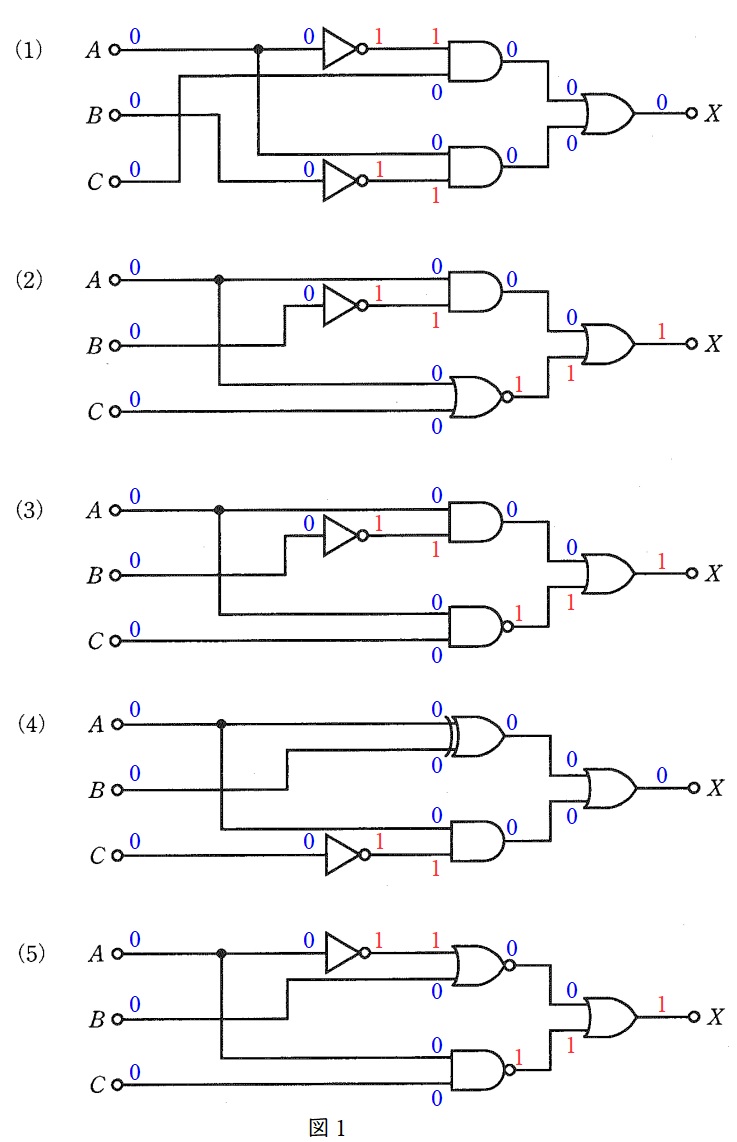
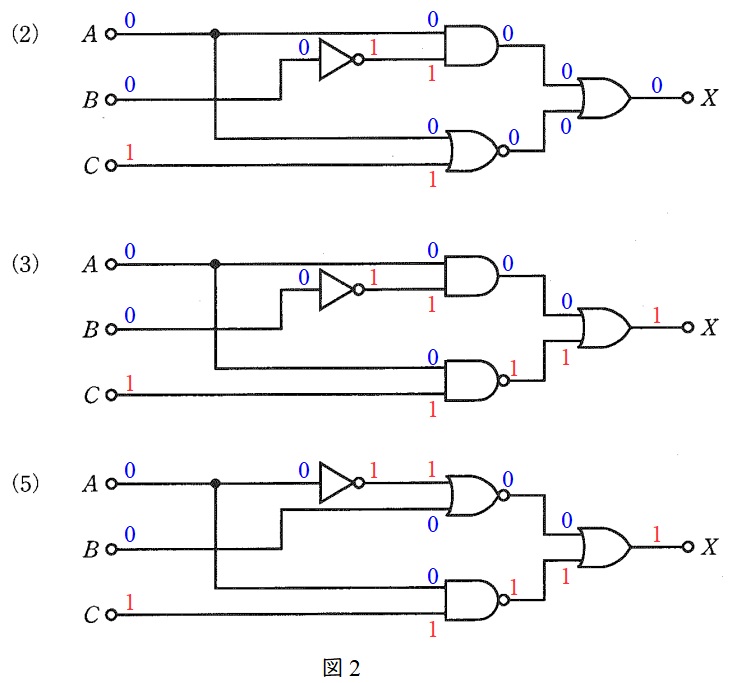
続いて,(2),(3),(5)の論理回路に\( \ A=0 \ \),\( \ B=0 \ \)及び\( \ C=1 \ \)を入力すると図2のようになり,出力\( \ X=0 \ \)となるのは(2)のみである。
したがって,解答は(2)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは