Contents
【問題】
【難易度】★★★☆☆(普通)
直流電動機の速度とトルクを次のように制御することを考える。
損失と電機子反作用を無視した場合,直流電動機では電機子巻線に発生する起電力は,界磁磁束と電機子巻線との相対速度に比例するので,\( \ \fbox { (ア) } \ \)では,界磁電流一定,すなわち磁束一定条件下で電機子電圧を増減し,電機子電圧に回転速度が\( \ \fbox { (イ) } \ \)するように回転速度を制御する。この電動機では界磁磁束一定条件下で電機子電流を増減し,電機子電流とトルクとが\( \ \fbox { (ウ) } \ \)するようにトルクを制御する。この電動機の高速運転では電機子電圧一定の条件下で界磁電流を増減し,界磁磁束に回転速度が\( \ \fbox { (エ) } \ \)するように回転速度を制御する。このように広い速度範囲で速度とトルクを制御できるので,\( \ \fbox { (ア) } \ \)は圧延機の駆動などに広く使われてきた。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 直巻電動機 & 反比例 & 比 例 & 比 例 \\
\hline
(2) & 直巻電動機 & 比 例 & 比 例 & 反比例 \\
\hline
(3) & 他励電動機 & 反比例 & 反比例 & 比 例 \\
\hline
(4) & 他励電動機 & 比 例 & 比 例 & 反比例 \\
\hline
(5) & 他励電動機 & 比 例 & 反比例 & 比 例 \\
\hline
\end{array}
\]
【ワンポイント解説】
直流電動機の速度制御とトルクに関する問題です。
問1から受験生の知識の幅を問うやや難易度な高めの問題です。
本問の内容は頭の中でなんとなく考えたり,結果を丸暗記するのではなく,等価回路や式変形をしっかりと行った上で解く方が良いかと思います。
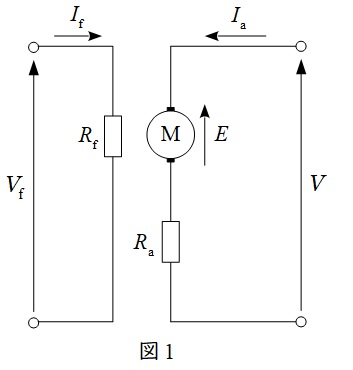
1.直流他励電動機の等価回路
図1に直流他励電動機の等価回路を示します。図1において,\( \ V \ \)は端子電圧,\( \ E \ \)は逆起電力,\( \ V_{\mathrm {f}} \ \)は界磁電圧,\( \ I_{\mathrm {a}} \ \)は電機子電流,\( \ I_{\mathrm {f}} \ \)は界磁電流,\( \ R_{\mathrm {a}} \ \)は電機子抵抗,\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては,界磁回路が独立しているので,界磁磁束を独立して制御できるという特徴があります。
また,上記の等価回路にキルヒホッフの法則を適用すると,以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
I_{\mathrm {f}} &=& \frac {V_{\mathrm {f}}}{R_{\mathrm {f}}} \\[ 5pt ]
\end{eqnarray}
\]
2.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),回転速度\( \ N \ \)とすると,直流機の誘導起電力(逆起電力)\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。
3.直流機のトルク\( \ T \ \)
磁極の数\( \ p \ \),電機子導体数\( \ Z \ \),電機子巻線並列回路数\( \ a \ \),各極の磁束\( \ \phi \ \),電機子電流\( \ I_{\mathrm {a}} \ \)とすると,直流機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\( \ \phi \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。
4.直流電動機の速度制御法
直流機の誘導起電力(逆起電力)の公式\( \ E=k_{\mathrm {e}}\phi N \ \)及び図1の等価回路より,直流機の誘導起電力(逆起電力)\( \ E \ \)について,
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N =V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,\( \ N \ \)について整理すると,
\[
\begin{eqnarray}
N &=&\frac {V-R_{\mathrm {a}}I_{\mathrm {a}}}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,回転速度\( \ N \ \)は,界磁\( \ \phi \ \),電機子抵抗\( \ R_{\mathrm {a}} \ \),電源電圧\( \ V \ \)でそれぞれ制御でき,それぞれ界磁制御法,抵抗制御法,電圧制御法と呼ばれます。
【解答】
解答:(4)
(ア)
問題文に「界磁電流一定,すなわち磁束一定条件下で電機子電圧を増減し」となっていることから,他励電動機となります。直巻電動機に関しては令和3年問1に記載がありますので,違いを理解しておくようにしましょう。
(イ)
ワンポイント解説「4.直流電動機の速度制御法」の通り,回転速度\( \ N \ \)は,
\[
\begin{eqnarray}
N &=&\frac {V-R_{\mathrm {a}}I_{\mathrm {a}}}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
となり,電機子電圧にほぼ比例します。
(ウ)
ワンポイント解説「3.直流機のトルク\( \ T \ \)」の通り,界磁磁束一定条件下においては,電機子電流とトルクとが比例します。
(エ)
ワンポイント解説「4.直流電動機の速度制御法」の通り,回転速度\( \ N \ \)は,
\[
\begin{eqnarray}
N &=&\frac {V-R_{\mathrm {a}}I_{\mathrm {a}}}{k_{\mathrm {e}}\phi } \\[ 5pt ]
\end{eqnarray}
\]
となり,界磁磁束に反比例します。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは