《機械》〈回転機〉[H24:問16]三相同期電動機の内部誘導起電力と負荷角に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

三相同期電動機が定格電圧\( \ 3.3 \ \mathrm {[kV]} \ \)で運転している。

ただし，三相同期電動機は星形結線で\( \ 1 \ \)相当たりの同期リアクタンスは\( \ 10 \ \mathrm {[\Omega ]} \ \)であり，電機子抵抗，損失及び磁気飽和は無視できるものとする。

次の(a)及び(b)の問に答えよ。

(a)　負荷電流（電機子電流）\( \ 110 \ \mathrm {[A]} \ \)，力率\(　\ \cos \ \varphi = 1 \ \)で運転しているときの\( \ 1 \ \)相当たりの内部誘導起電力\( \ \mathrm {[V]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1 \ 100 \ \)　　(2)　\( \ 1 \ 600 \ \)　　(3)　\( \ 1 \ 900 \ \)　　(4)　\( \ 2 \ 200 \ \)　　(5)　\( \ 3 \ 300 \ \)

(b)　上記(a)の場合と電圧及び出力は同一で，界磁電流を\( \ 1.5 \ \)倍に増加したときの負荷角（電動機端子電圧と内部誘導起電力との位相差）を\( \ \delta ^{\prime } \ \)とするとき，\( \ \sin \delta ^{\prime } \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.250 \ \)　　(2)　\( \ 0.333 \ \)　　(3)　\( \ 0.500 \ \)　　(4)　\( \ 0.707 \ \)　　(5)　\( \ 0.866 \ \)

【ワンポイント解説】

まずは等価回路とベクトル図が描けるかどうかがポイントとなります。一般に同期機は同期発電機から出題されますが、本問は同期電動機です。本問で違いをよく理解しておくようにしましょう。

1.同期電動機の等価回路
電動機の端子電圧（電源電圧）を\( \ \dot V \ \)，誘導起電力を\( \ \dot E \ \)，同期リアクタンスを\( \ x_{\mathrm {s}} \ \)，電機子電流を\( \ \dot I \ \)とすると，同期発電機の等価回路は図1のように描くことができます。

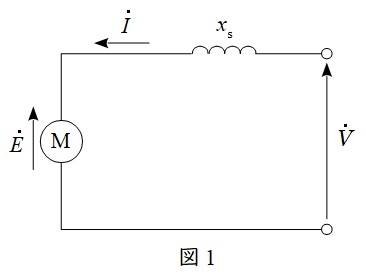
2.同期電動機の出力
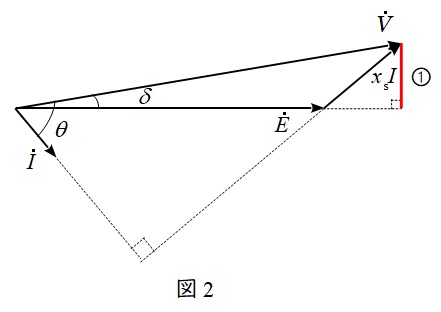
図2のように，\( \ 1 \ \)相分の誘導起電力\( \ E \ \mathrm {[V]} \ \)，電圧\( \ V \ \mathrm {[V]} \ \)，電流\( \ I \ \mathrm {[A]} \ \)，\( \ E \ \)と\( \ V \ \)の位相差（負荷角）を\( \ \delta \ \mathrm {[rad]} \ \)，\( \ V \ \)と\( \ I \ \)の位相差を\( \ \theta \ \mathrm {[rad]} \ \)とすると，\( \ 1 \ \)相分の出力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&EI\cos \left( \theta -\delta \right) \\[ 5pt ] \end{eqnarray}
\] で求められ，図2の①の赤線を求める式より，
\[
\begin{eqnarray}
x_{\mathrm {s}}I\cos \left( \theta -\delta \right) &=&V\sin \delta \\[ 5pt ] I\cos \left( \theta -\delta \right) &=&\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
P &=&EI\cos \left( \theta -\delta \right) \\[ 5pt ] &=&E\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] &=&\frac {VE}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] と求められます。

　※この式は同期機出力の基本式として暗記しておきましょう。

【解答】

(a)解答：(4)
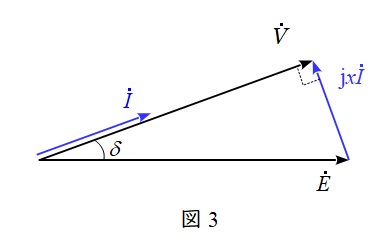
力率\(　\ \cos \ \varphi = 1 \ \)であり，電源電圧\( \ \dot V \ \)と負荷電流（電機子電流）\( \ \dot I \ \)の位相差はないので、１相分の等価回路を描くと図3のようになる。
図3において，電源電圧の大きさ\( \ \displaystyle V=\frac {3300}{\sqrt {3}} \ \mathrm {[V]} \ \)，負荷電流の大きさ\( \ \displaystyle I=110 \ \mathrm {[A]} \ \)，同期リアクタンスの大きさ\( \ x_{\mathrm {s}}=10 \ \mathrm {[\Omega ]} \ \)であるから，三平方の定理より，
\[
\begin{eqnarray}
E &=&\sqrt {V^{2}+\left( x_{\mathrm {s}}I\right) ^{2} } \\[ 5pt ] &=&\sqrt {\left( \frac {3300}{\sqrt {3}}\right) ^{2}+\left( 10\times 110\right) ^{2} } \\[ 5pt ] &=&\sqrt {3630000+1210000} \\[ 5pt ] &=&2200 \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
同期機の誘導起電力\( \ E \ \)は，周波数を\( \ f \ \)，1相の直列巻数を\( \ w \ \)，1極あたりの磁束を\( \ \phi \ \)とすると，
\[
\begin{eqnarray}
E &=&4.44kfw\phi \\[ 5pt ] \end{eqnarray}
\] で与えられ，さらに\( \ N \phi = LI \ \)の関係から，\( \ \phi \ \)は界磁電流に比例するので，誘導起電力\( \ E \ \)は界磁電流に比例する。したがって，界磁電流を\( \ 1.5 \ \)倍に増加したときの誘導起電力の大きさ\( \ E^{\prime } \ \)は，
\[
\begin{eqnarray}
E^{\prime } &=&1.5E \\[ 5pt ] &=&1.5\times 2200 \\[ 5pt ] &=&3300 \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。(a)の場合と電圧及び出力は同一であるので，図3より，1相分の出力の大きさ\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&EI\cos \delta \\[ 5pt ] &=&EI\times \frac {V}{E} \\[ 5pt ] &=&VI \\[ 5pt ] &=&\frac {3300}{\sqrt {3}}\times 110 \\[ 5pt ] &≒&209600 \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.同期電動機の出力」より，
\[
\begin{eqnarray}
P &=&\frac {VE^{\prime } }{x_{\mathrm {s}}}\sin \delta ^{\prime } \\[ 5pt ] \sin \delta ^{\prime }&=&\frac {Px_{\mathrm {s}}}{VE^{\prime } } \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
\sin \delta ^{\prime }&=&\frac {209600\times 10}{\displaystyle \frac {3300}{\sqrt {3}}\times 3300} \\[ 5pt ] &≒&\frac {2096000}{6287000} \\[ 5pt ] &≒&0.333 \\[ 5pt ] \end{eqnarray}
\] と求められる。

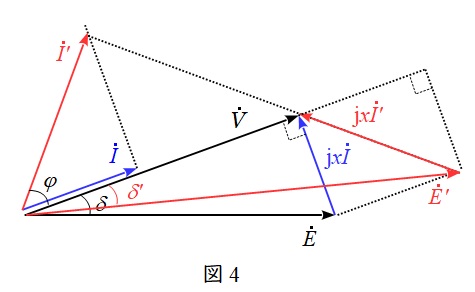
　※参考図（(b)の条件の時のベクトル図）