《機械》〈変圧器〉[H25:問15]変圧器の無負荷試験及び短絡試験に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

定格容量$\ 10 \ \mathrm {[kV\cdot A]} \ $，定格一次電圧$\ 1000 \ \mathrm {[V]} \ $，定格二次電圧$\ 100 \ \mathrm {[V]} \ $の単相変圧器で無負荷試験及び短絡試験を実施した。高圧側の回路を開放して低圧側の回路に定格電圧を加えたところ，電力計の指示は$\ 80 \ \mathrm {[W]} \ $であった。次に，低圧側の回路を短絡して高圧側の回路にインピーダンス電圧を加えて定格電流を流したところ，電力計の指示は$\ 120 \ \mathrm {[W]} \ $であった。

(a)　巻線の高圧側換算抵抗$\ \mathrm {[\Omega ]} \ $の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$1.0$　　(2)　$1.2$　　(3)　$1.4$　　(4)　$1.6$　　(5)　$2.0$

(b)　力率$\ \cos \phi =1 \ $の定格運転時の効率$\ \mathrm {[％]} \ $の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$95$　　(2)　$96$　　(3)　$97$　　(4)　$98$　　(5)　$99$

【ワンポイント解説】

変圧器の無負荷試験と短絡試験では，それぞれ鉄損及び銅損が求められます。二種の二次試験でも出題されるような問題でやや難しい印象があるかもしれませんが，損失や効率を理解する上で必要な知識となります。変圧器の等価回路を基本に，無負荷試験と短絡試験の等価回路を描けるようにしておきましょう。

1.変圧器の等価回路（一次換算）
変圧器の一次側等価回路を図1に示します。ただし，$\ {\dot V}_{1} \ $は一次側端子電圧，$\ {\dot I}_{1} \ $は一次電流，$\ {\dot I}_{2} \ $は二次電流，$\ {\dot I}_{0} \ $は励磁電流，$\ r_{1} \ $は一次巻線抵抗，$\ r_{2} \ $は二次巻線抵抗，$\ x_{1} \ $は一次漏れリアクタンス，$\ x_{2} \ $は二次漏れリアクタンス，$\ a \ $は変圧比（巻数比）となります。

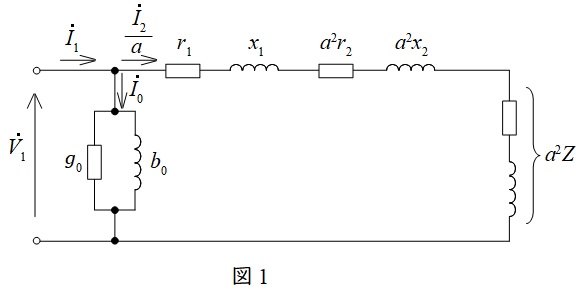
2.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス$\ g_{0} \ $及び励磁サセプタンス$\ b_{0} \ $を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

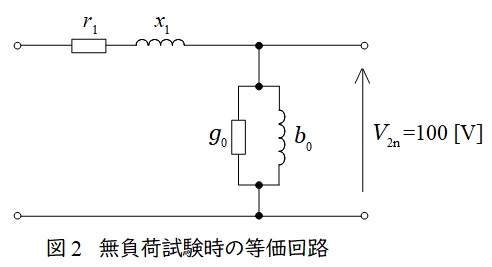
3.短絡試験の等価回路
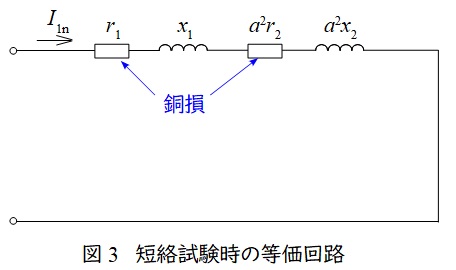
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は銅損となります。測定される電力と電流から，高圧側換算の巻線抵抗$\ R=r_{1}+a^{2}r_{2} \ $を求めることが可能となります

4.変圧器の効率
変圧器の規約効率$\ \eta \ $は次式で求められます。
$$\begin{eqnarray} \eta &=& \frac {出力}{入力} \\[ 5pt ] &=& \frac {出力}{出力＋損失} \\[ 5pt ] \end{eqnarray}$$

【関連する「電気の神髄」記事】

　　変圧器の効率

【解答】

(a)解答：(2)
巻線の高圧側換算抵抗は短絡試験の結果より求められる。
図3の回路において，定格一次電流$\ I_{\mathrm {1n}} \ $の大きさは，
$$\begin{eqnarray} I_{\mathrm {1n}} &=& \frac {10\times 10^{3}}{1000} \\[ 5pt ] &=& 10 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ であり，短絡試験の電力計の指示が$\ 120 \ \mathrm {[W]} \ $であるため，一次巻線抵抗$\ r_{1} \ $，二次巻線抵抗$\ r_{2} \ $の一次換算値の合計の消費電力と一致する。したがって，
$$\begin{eqnarray} \left( r_{1}+a^{2}r_{2}\right) {I_{\mathrm {1n}}}^{2} &=& 120 \\[ 5pt ] \left( r_{1}+a^{2}r_{2}\right) \times 10^{2} &=& 120 \\[ 5pt ] r_{1}+a^{2}r_{2}&=& 1.2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(b)解答：(4)
各試験結果から，鉄損$\ P_{\mathrm {i}}=80 \ \mathrm {[W]} \ $，銅損$\ P_{\mathrm {c}}=120 \ \mathrm {[W]} \ $である。
ワンポイント解説「4.変圧器の効率」より，力率$\ \cos \phi =1 \ $の定格運転時の効率$\ \eta \ $は，
$$\begin{eqnarray} \eta &=& \frac {P_{\mathrm {n}}}{P_{\mathrm {n}}+P_{\mathrm {i}}+P_{\mathrm {c}}} \\[ 5pt ] &=& \frac {10\times 10^{3}}{10\times 10^{3}+80+120} \\[ 5pt ] &≒&0.98　→　98 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。