《機械》〈回転機〉[H26:問2]直流発電機と電動機の負荷電流に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

出力\(20 \ \mathrm {kW}\)，端子電圧\(100 \ \mathrm {V}\)，回転速度\(1500 \ \mathrm {{min}^{-1}}\)で運転していた直流他励発電機があり，その電機子回路の抵抗は\(0.05 \ \mathrm {\Omega }\)であった。この発電機を電圧\(100 \ \mathrm {V}\)の直流電源に接続して，そのまま直流他励電動機として使用したとき，ある負荷で回転速度は\(1200 \ \mathrm {{min}^{-1}}\)となり安定した。

このときの運転状態における電動機の負荷電流(電機子電流)の値\(\mathrm {[A]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，発電機での運転と電動機での運転とで，界磁電圧は変わらないものとし，ブラシの接触による電圧降下及び電機子反作用は無視できるものとする。

　(1)　180　　(2)　200　　(3)　220　　(4)　240　　(5)　260

【ワンポイント解説】

本問のような問題は等価回路を描けば，あとは簡単な回路計算となります。等価回路は確実に描けるようにして下さい。

1.他励発電機，電動機の等価回路
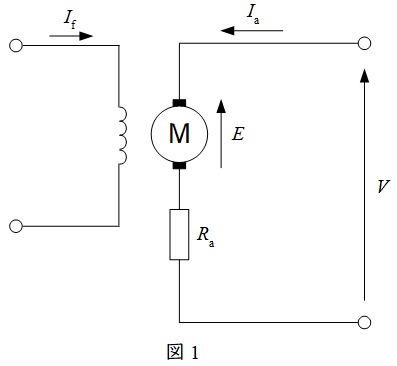
他励電動機の等価回路を図1に示します。ここで\(V\)は端子電圧，\(E\)は逆起電力，\(I_{\mathrm {f}}\)は界磁電流，\(I_{\mathrm {a}}\)は電機子電流，\(R_{\mathrm {a}}\)は電機子抵抗となります。発電機として使用する時は，電機子電流\(I_{\mathrm {a}}\)の向きが逆となり，\(E\)の名称が誘導起電力となります。

2.直流機の誘導起電力の大きさ
電機子巻線の並列回路数を\(a\)，磁極数を\(p\)，電機子の導体数を\(Z\)，磁束を\(\phi \)，回転速度を\(N\)とすると，誘導起電力の大きさ\(E\)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] ⇔　E&∝&N \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
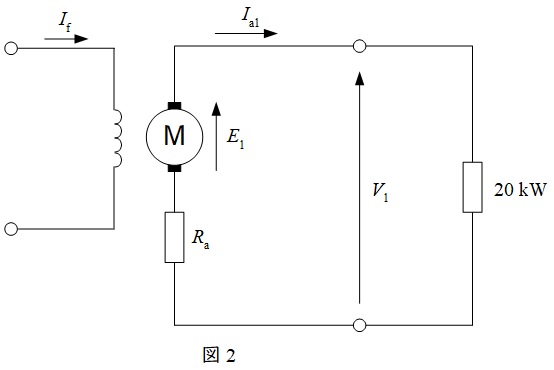
題意に沿って，発電機として使用したときの等価回路を図2，電動機として使用したときの等価回路を図3に示す。図2において，出力\(P=20 \ \mathrm {kW}\)，端子電圧\(V_{1}=100 \ \mathrm {V}\)であるから，電機子電流\(I_{\mathrm {a1}}\)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {a1}} &=&\frac {P}{V_{1}} \\[ 5pt ] &=&\frac {20\times 10^{3}}{100} \\[ 5pt ] &=&200 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，誘導起電力\(E_{1}\)の大きさは，電機子抵抗\(R_{\mathrm {a}}\)での電圧降下を考慮すると，
\[
\begin{eqnarray}
E_{1} &=&V_{1}+R_{\mathrm {a}}I_{\mathrm {a1}} \\[ 5pt ] &=&100+0.05\times 200 \\[ 5pt ] &=&110 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
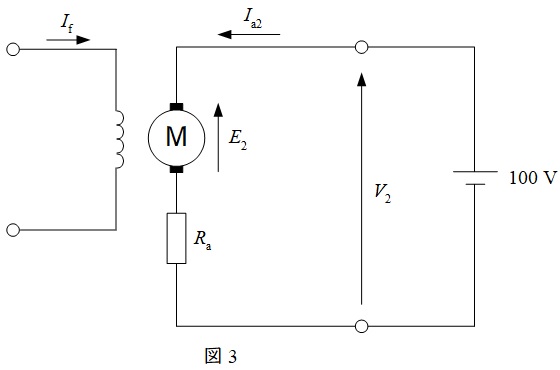
\] となる。ワンポイント解説「2.直流機の誘導起電力の大きさ」より，誘導起電力の大きさと回転数は比例するので，図3のように電動機として使用した時の逆起電力の大きさ\(E_{2}\)は，
\[
\begin{eqnarray}
\frac {E_{1}}{E_{2}} &=&\frac {N_{1}}{N_{2}} \\[ 5pt ] \frac {110}{E_{2}} &=&\frac {1500}{1200} \\[ 5pt ] E_{2}&=&88 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，電機子抵抗\(R_{\mathrm {a}}\)にかかる電圧は\(12 \ \mathrm {V}\)となるから，電機子電流\(I_{\mathrm {a2}}\)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {a2}} &=&\frac {12}{R_{\mathrm {a}}} \\[ 5pt ] &=&\frac {12}{0.05} \\[ 5pt ] &=&240 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。