《機械》〈自動制御〉[R4上:問15]一巡伝達関数及びナイキスト線図に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図は，出力信号\( \ y \ \)を入力信号\( \ x \ \)に一致させるように動作するフィードバック制御系のブロック線図である。次の(a)及び(b)の問に答えよ。

(a)　図において，\( \ K=5 \ \)，\( \ T=0.1 \ \)として，入力信号からフィードバック信号までの一巡伝達関数(開ループ伝達関数)を表す式を計算し，正しいものを次の(1)～(5)から一つ選べ。

　(1)　\( \ \displaystyle \frac {5}{1-\mathrm {j}\omega 0.1} \ \)　　(2)　\( \ \displaystyle \frac {5}{1+\mathrm {j}\omega 0.1} \ \)　　(3)　\( \ \displaystyle \frac {1}{6+\mathrm {j}\omega 0.1} \ \)

　(4)　\( \ \displaystyle \frac {5}{6-\mathrm {j}\omega 0.1} \ \)　　(5)　\( \ \displaystyle \frac {5}{6+\mathrm {j}\omega 0.1} \ \)

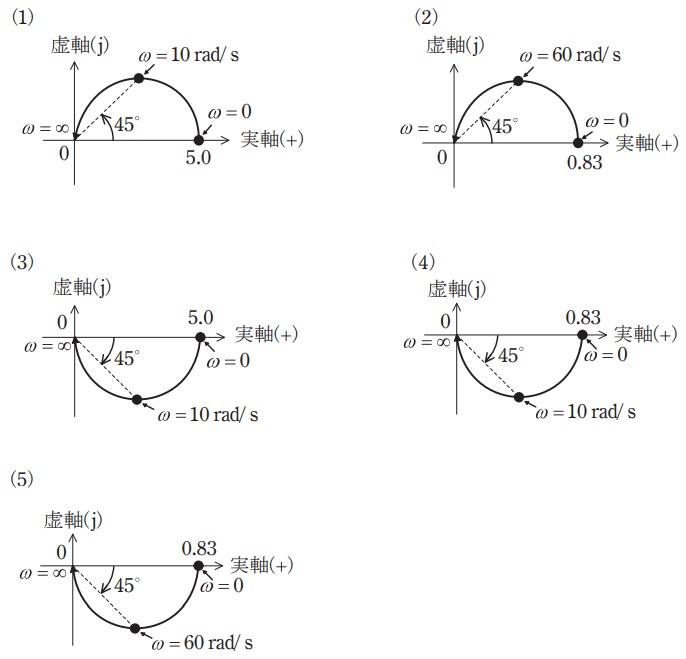
(b)　(a)で求めた一巡伝達関数において， \( \ \omega \ \)を変化させることで得られるベクトル軌跡はどのような曲線を描くか，最も近いものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

フィードバック制御の伝達関数の導出とナイキスト線図の作図に関する問題です。
問題の難易度はそれほど高くありませんが，閉ループ伝達関数を計算し(a)を別の選択肢を選択してしまうと(b)も連動して間違えてしまいます。
ナイキスト線図を描くときには一巡伝達関数を使用することを覚えておいて下さい。

1.開ループ伝達関数と閉ループ伝達関数
ブロック線図において，フィードバック制御のループを考慮しない関数を開ループ伝達関数，ループを考慮する関数を閉ループ伝達関数，ループを一巡だけ考慮する関数を一巡伝達関数といいます。
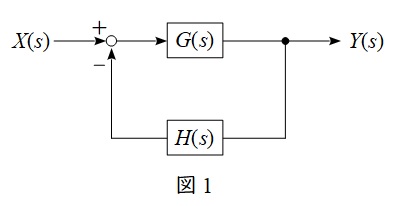
図1の例においては，開ループ伝達関数\( \ W_{\mathrm {o}} \left( s \right) \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {o}} \left( s \right) &=& G \left( s \right) \\[ 5pt ] \end{eqnarray}
\] 閉ループ伝達関数\( \ W \left( s \right) \ \)は，
\[
\begin{eqnarray}
W \left( s \right) &=&\frac {G \left( s \right) }{1+G \left( s \right) H \left( s \right) } \\[ 5pt ] \end{eqnarray}
\] 一巡伝達関数\( \ W_{\mathrm {r}} \left( s \right) \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {r}} \left( s \right) &=& G \left( s \right) H \left( s \right) \\[ 5pt ] \end{eqnarray}
\] となります。

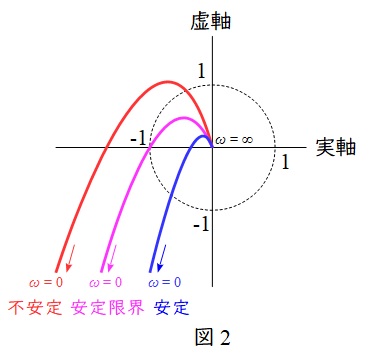
2.ナイキストの安定判別法
図2に示すような周波数伝達関数のベクトル軌跡をナイキスト線図といい，ナイキスト線図による安定判別をナイキストの安定判別法といいます。
一巡伝達関数\( \ W_{\mathrm {r}} \left( \mathrm {j}\omega \right) \ \)において，角周波数\( \ \omega \ \)を\( \ 0 \ \)から\( \ \infty \ \)まで変化させたときのベクトル軌跡を描いたとき，
　実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)より右側であれば安定
　実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)であれば安定限界
　実軸との交点が\( \left( -1 , \mathrm {j}0\right) \)より左側であれば不安定
となります。

【解答】

(a)解答：(2)
制御器\( \ K \ \)の出口の信号を\( \ U \left( \mathrm {j}\omega \right) \ \)とする。制御対象の伝達関数を\( \ G \left( \mathrm {j}\omega \right) \ \)とすると，
\[
\begin{eqnarray}
\left\{ U \left( \mathrm {j}\omega \right)-Y \left( \mathrm {j}\omega \right) \right\}\frac {1}{\mathrm {j}\omega T} &=& Y \left( \mathrm {j}\omega \right) \\[ 5pt ] U \left( \mathrm {j}\omega \right)-Y \left( \mathrm {j}\omega \right) &=& \mathrm {j}\omega TY \left( \mathrm {j}\omega \right) \\[ 5pt ] U \left( \mathrm {j}\omega \right) &=& Y \left( \mathrm {j}\omega \right) +\mathrm {j}\omega TY \left( \mathrm {j}\omega \right) \\[ 5pt ] U \left( \mathrm {j}\omega \right) &=& \left( 1+\mathrm {j}\omega T \right) Y \left( \mathrm {j}\omega \right) \\[ 5pt ] \frac {Y \left( \mathrm {j}\omega \right) }{U \left( \mathrm {j}\omega \right) }&=& \frac {1}{1+\mathrm {j}\omega T } \\[ 5pt ] G \left( \mathrm {j}\omega \right) &=& \frac {1}{1+\mathrm {j}\omega T } \\[ 5pt ] \end{eqnarray}
\] となるから，入力信号\( \ X \left( \mathrm {j}\omega \right) \ \)からフィードバック信号\( \ Y \left( \mathrm {j}\omega \right) \ \)までの一巡伝達関数\( \ W_{\mathrm {r}} \left( \mathrm {j}\omega \right) \ \)は，
\[
\begin{eqnarray}
Y \left( \mathrm {j}\omega \right) &=& KG \left( \mathrm {j}\omega \right) X \left( \mathrm {j}\omega \right) \\[ 5pt ] &=& K\cdot \frac {1}{1+\mathrm {j}\omega T }X \left( \mathrm {j}\omega \right) \\[ 5pt ] \frac {Y \left( \mathrm {j}\omega \right) }{X \left( \mathrm {j}\omega \right) }&=& \frac {K}{1+\mathrm {j}\omega T } \\[ 5pt ] W_{\mathrm {r}} \left( \mathrm {j}\omega \right) &=& \frac {K}{1+\mathrm {j}\omega T } \\[ 5pt ] \end{eqnarray}
\] となり，\( \ K=5 \ \)，\( \ T=0.1 \ \)を代入すると，
\[
\begin{eqnarray}
W_{\mathrm {r}} \left( \mathrm {j}\omega \right) &=& \frac {5}{1+\mathrm {j}\omega 0.1 } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
(a)で求めた一巡伝達関数\( \ W_{\mathrm {r}} \left( \mathrm {j}\omega \right) \ \)について，
\[
\begin{eqnarray}
\displaystyle \lim_{ \omega \to \infty } W_{\mathrm {r}} \left( \mathrm {j}\omega \right) &=& \displaystyle \lim_{ \omega \to \infty } \left( \frac {5}{1+\mathrm {j}\omega 0.1 }\right) \\[ 5pt ] &=& 0 \\[ 5pt ] \displaystyle \lim_{ \omega \to 0 } W_{\mathrm {r}} \left( \mathrm {j}\omega \right) &=& \displaystyle \lim_{ \omega \to 0 } \left( \frac {5}{1+\mathrm {j}\omega 0.1 }\right) \\[ 5pt ] &=& \frac {5}{1+\mathrm {j}\times 0\times 0.1} \\[ 5pt ] &=& 5.0 \\[ 5pt ] W_{\mathrm {r}} \left( \mathrm {j}10 \right) &=& \frac {5}{1+\mathrm {j}\times 10\times 0.1 } \\[ 5pt ] &=& \frac {5}{1+\mathrm {j}} \\[ 5pt ] &=& \frac {5}{1+\mathrm {j}}\times \frac {1-\mathrm {j}}{1-\mathrm {j}} \\[ 5pt ] &=& \frac {5}{2}\left( 1-\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] となるので，最も適当なのは(3)と求められる。