《機械》〈制御〉[H27:問17]フィードバック制御の伝達関数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図に示すように，フィードバック接続を含んだブロック線図がある。このブロック線図において，\( \ T=0.2 \ \mathrm {s} \ \)，\( \ K=10 \ \)としたとき，次の(a)及び(b)の問に答えよ。

ただし，\( \ \omega \ \)は角周波数\( \ \mathrm {rad/s} \ \)を表す。

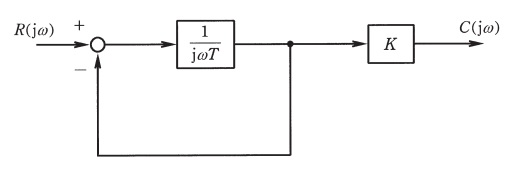
(a)　入力を\( \ R(\mathrm {j}\omega ) \ \)，出力を\( \ C(\mathrm {j}\omega ) \ \)とする全体の周波数伝達関数\( \ W(\mathrm {j}\omega ) \ \)として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \displaystyle \frac {10}{1+\mathrm {j}0.2\omega } \ \)　　(2)　\( \ \displaystyle \frac {1}{1+\mathrm {j}0.2\omega } \ \)　　(3)　\( \ \displaystyle \frac {1}{1+\mathrm {j}5\omega } \ \)

　(4)　\( \ \displaystyle \frac {50\omega }{1+\mathrm {j}5\omega } \ \)　　　(5)　\( \ \displaystyle \frac {\mathrm {j}2\omega }{1+\mathrm {j}0.2\omega } \ \)

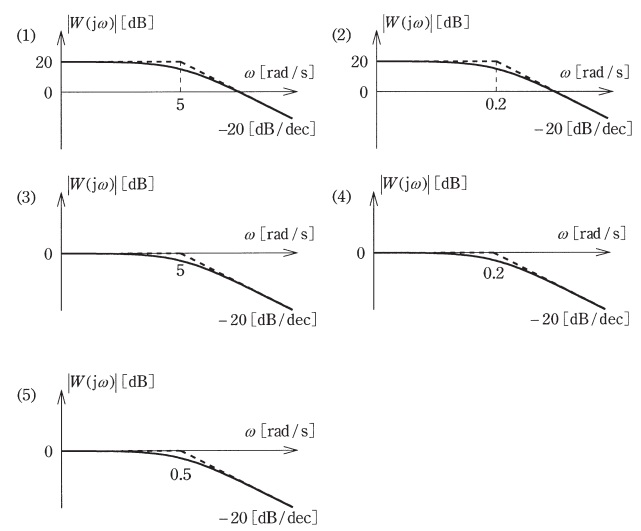
(b)　次のボード線図には，正確なゲイン特性を実線で，その折線近似ゲイン特性を破線で示し，横軸には特に折れ点角周波数の数値を示している。上記(a)の周波数伝達関数\( \ W(\mathrm {j}\omega ) \ \)のボード線図のゲイン特性として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，横軸は角周波数\( \ \omega \ \)の対数軸であり，\( \ -20 \ \mathrm{[dB/dec]} \ \)とは，\( \ \omega \ \)が10倍大きくなるに従って\( \ \left| W(j\omega ) \right| \ \)が\( \ -20 \ \mathrm{dB} \ \)変化する傾きを示している。

【ワンポイント解説】

自動制御の問題は毎年1問程度出題されます。二種では二次試験にも必ず出題される上位資格に繋がる内容なので，是非理解するようにしましょう。

1.ブロック線図の等価変換
①直列
図1のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
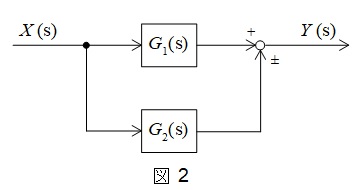
図2のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

③フィードバック
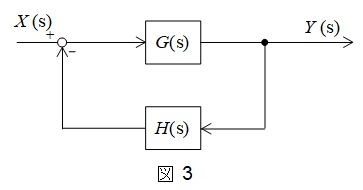
図3のような\( \ G(s) \ \)，\( \ H(s) \ \)が与えられているとき，全体の伝達関数\( \ W(s) \ \)は，
\[
\begin{eqnarray}
Y(s)&=&\left( X(s) -H(s)Y(s) \right) G(s) \\[ 5pt ] Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ] Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ] \left( 1+G(s)H(s)\right) Y(s) &=&G(s)X(s) \\[ 5pt ] \frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] \end{eqnarray}
\] となります。

2.周波数伝達関数のゲイン
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {1}{1+\mathrm {j}\omega T} \ \)で与えられる時，この周波数伝達関数の絶対値\( \ \left| W(\mathrm {j}\omega ) \right| \ \)は，
\[
\begin{eqnarray}
\left| W(\mathrm {j}\omega ) \right| &=&\left| \frac {1}{1+\mathrm {j}\omega T}\right| \\[ 5pt ] &=&\frac {1}{\sqrt {1+\left( \omega T\right) ^{2}}} \\[ 5pt ] &=&\frac {1}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ] \end{eqnarray}
\] となり，この周波数伝達関数のゲイン\( \ g \ \)は
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \frac {1}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ] &=&20\log _{10} 1-20\log _{10} \sqrt {1+\omega ^{2}T^{2}} \\[ 5pt ] &=&0-10\log _{10} \left( 1+\omega ^{2}T^{2}\right) \\[ 5pt ] &=&-10\log _{10} \left( 1+\omega ^{2}T^{2}\right) \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(1)
問題図の中間点の引出部の関数を\(X(\mathrm {j}\omega )\)とすると，ワンポイント解説「1.ブロック線図の等価変換」より，
\[
\begin{eqnarray}
\frac {X(\mathrm {j}\omega )}{R(j\omega )}&=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega T}}{1+\displaystyle \frac {1}{\mathrm {j}\omega T}} \\[ 5pt ] &=&\frac {1}{1+\mathrm {j}\omega T} \\[ 5pt ] \frac {C(\mathrm {j}\omega )}{X(j\omega )}&=&K
\end{eqnarray}
\] であるから，周波数伝達関数\(W(\mathrm {j}\omega )\)は，
\[
\begin{eqnarray}
W(\mathrm {j}\omega )&=&\frac {C(\mathrm {j}\omega )}{R(\mathrm {j}\omega )} \\[ 5pt ] &=&\frac {C(\mathrm {j}\omega )}{X(\mathrm {j}\omega )} \frac {X(\mathrm {j}\omega )}{R(\mathrm {j}\omega )} \\[ 5pt ] &=&\frac {K}{1+\mathrm {j}\omega T} \\[ 5pt ] &=&\frac {10}{1+\mathrm {j}0.2\omega } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
ワンポイント解説「2.周波数伝達関数のゲイン」より，周波数伝達関数\(W(\mathrm {j}\omega )\)のゲイン\(g\)は，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ] &=&20\log _{10} \left| \frac {10}{1+\mathrm {j}0.2\omega }\right| \\[ 5pt ] &=&20\log _{10} \frac {10}{\sqrt{ 1^{2}+(0.2\omega )^{2}}} \\[ 5pt ] &=&20\log _{10} \frac {10}{\sqrt{ 1+0.04\omega ^{2} }}\\[ 5pt ] \end{eqnarray}
\] となる。ここで，ゲイン\(g\)に\(\omega =0\)を代入すると，
\[
\begin{eqnarray}
g (0) &=&20\log _{10} \frac {10}{\sqrt{ 1+0.04\times 0^{2} }} \\[ 5pt ] &=&20\log _{10} 10 \\[ 5pt ] &=&20 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}
\] となり，\(g=0\)を代入すると，
\[
\begin{eqnarray}
0&=&20\log _{10} \frac {10}{\sqrt{ 1+0.04\omega ^{2} }} \\[ 5pt ] 0&=&\log _{10} \frac {10}{\sqrt{ 1+0.04\omega ^{2} }} \\[ 5pt ] \frac {10}{\sqrt{ 1+0.04\omega ^{2} }}&=&1 \\[ 5pt ] \sqrt{ 1+0.04\omega ^{2} }&=&10 \\[ 5pt ] 1+0.04\omega ^{2}&=&100 \\[ 5pt ] \omega &=&49.7 \ \mathrm {[rad/s]} \\[ 5pt ] \end{eqnarray}
\] となり，最も適当なのは(1)であることが分かる。