《機械》〈照明〉[H27:問16]LEDによる光度及び照度の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

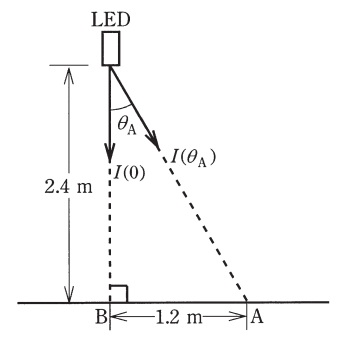
図に示すように，\( \ \mathrm {LED} \ \)\( \ 1 \ \)個が，床面から高さ\( \ \mathrm {2.4 \ m} \ \)の位置で下向きに取り付けられ，点灯している。この\( \ \mathrm {LED} \ \)の直下方向となす角(鉛直角)を\( \ \theta \ \)とすると，この\( \ \mathrm {LED} \ \)の配光特性(\( \ \theta \ \)方向の光度\( \ I(\theta ) \ \))は，\( \ \mathrm {LED} \ \)直下方向光度\( \ I( 0 ) \ \)を用いて\( \ I(\theta ) =I( 0 )\cos \theta \ \)で表されるものとする。次の(a)及び(b)の問に答えよ。

(a)　床面\( \ \mathrm {A} \ \)点における照度が\( \ 20 \ \mathrm {lx} \ \)であるとき，\( \ \mathrm {A} \ \)点がつくる鉛直角\( \ \theta _{\mathrm {A}} \ \)の方向の光度\( \ I(\theta _{\mathrm {A}} ) \ \)の値\( \ \mathrm {[cd]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　ただし，この\( \ \mathrm {LED} \ \)以外に光源はなく，天井や壁など，周囲からの反射光の影響もないものとする。

　　　

　(1)　\( \ 60 \ \)　　(2)　\( \ 119 \ \)　　(3)　\( \ 144 \ \)　　(4)　\( \ 160 \ \)　　(5)　\( \ 319 \ \)

(b)　この\( \ \mathrm {LED} \ \)直下の床面\( \ \mathrm {B} \ \)点の照度の値\( \ \mathrm {[lx]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 25 \ \)　　(2)　\( \ 28 \ \)　　(3)　\( \ 31 \ \)　　(4)　\( \ 49 \ \)　　(5)　\( \ 61 \ \)

【ワンポイント解説】

水平面照度に関する問題です。照明分野の計算問題としては，最も出題されやすい問題と言えると思います。

1.逆\( \ 2 \ \)乗の法則
照度\( \ E \ \)と光度\( \ I \ \)と光源からの距離\( \ r \ \)の間に，
\[
E=\frac {I}{r^{2}}
\] が成立するという法則です。

2.水平面照度
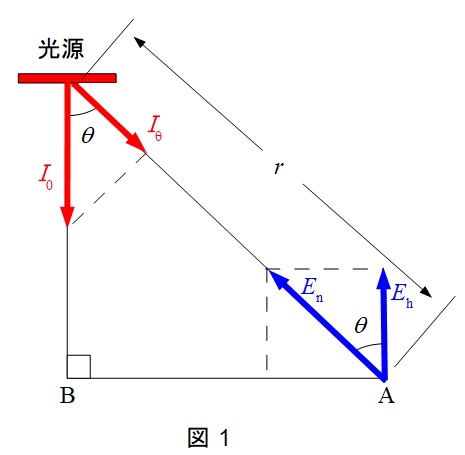
図1における\( \ E_{\mathrm {n}} \ \)を法線照度，\( \ E_{\mathrm {h}} \ \)を水平面照度と言い，下式のような関係があります。照度計で測定される\( \ \mathrm {A} \ \)点の照度は水平面照度\( \ E_{\mathrm {h}} \ \)になります。
\[
E_{\mathrm {n}}=\frac {I_{\theta }}{r^{2}}
\] \[
E_{\mathrm {h}}=E_{\mathrm {\mathrm {n}}}\cos\theta =\frac {I_{\theta }\cos\theta }{r^{2}}
\]

【解答】

(a)解答：(4)
\( \ \mathrm {LED} \ \)から\( \ \mathrm {A} \ \)点までの距離\( \ r \ \)は，三平方の定理から，
\[
\begin{eqnarray}
r&=&\sqrt {2.4^{2} +1.2^{2}} \\[ 5pt ] &≒&2.683 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ \cos \theta _{\mathrm {A}} \ \)は，
\[
\begin{eqnarray}
\cos \theta _{\mathrm {A}}&=&\frac {2.4}{r} \\[ 5pt ] &=&\frac {2.4}{2.683} \\[ 5pt ] &≒&0.8945 \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「2.水平面照度」より，鉛直角\( \ \theta _{\mathrm {A}} \ \)の方向の光度\( \ I(\theta _{\mathrm {A}} ) \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {h}}&=&\frac {I(\theta _{\mathrm {A}} )\cos\theta _{\mathrm {A}}}{r^{2}} \\[ 5pt ] 20&=&\frac {I(\theta _{\mathrm {A}} )\times 0.8945}{2.683^{2}} \\[ 5pt ] I(\theta _{\mathrm {A}} )&≒&161.0　→　160 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
題意より，\( \ \mathrm {LED} \ \)直下方向の光度\( \ I(0) \ \)は，
\[
\begin{eqnarray}
I(\theta _{\mathrm {A}} )&=&I(0)\cos\theta _{\mathrm {A}} \\[ 5pt ] 161.0&=&I(0)\times 0.8945 \\[ 5pt ] I(0)&≒&180.0 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「1.逆2乗の法則」より，床面\( \ \mathrm {B} \ \)点の照度\( \ E_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {B}}&=&\frac {I(0)}{2.4^{2}}\\[ 5pt ] &=&\frac {180.0}{2.4^{2}}\\[ 5pt ] &=&31.25　→　31 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。