《機械》〈回転機〉[H28:問15]同期発電機の電圧計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

定格出力\( \ 3300 \ \mathrm {kV\cdot A} \ \)，定格電圧\( \ 6600 \ \mathrm {V} \ \)，定格力率\( \ 0.9 \ \)(遅れ)の非突極形三相同期発電機があり，星形接続\( \ 1 \ \)相当たりの同期リアクタンスは\( \ 12.0 \ \mathrm {\Omega } \ \)である。電機子の巻線抵抗及び磁気回路の飽和は無視できるものとして，次の(a)及び(b)の問に答えよ。

(a)　定格運転時における\( \ 1 \ \)相当たりの内部誘導起電力の値\( \ \mathrm {[ V ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3460 \ \)　　(2)　\( \ 3810 \ \)　　(3)　\( \ 6170 \ \)　　(4)　\( \ 7090 \ \)　　(5)　\( \ 8690 \ \)

(b)　上記の発電機の励磁を定格状態に保ったまま運転し，星形結線\( \ 1 \ \)相当たりのインピーダンスが\( \ \mathrm {13+\mathrm {j}5\Omega } \ \)の平衡三相誘導性負荷を接続した。このときの発電機端子電圧の値\( \ \mathrm {[ V ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3810 \ \)　　(2)　\( \ 4010 \ \)　　(3)　\( \ 5990 \ \)　　(4)　\( \ 6600 \ \)　　(5)　\( \ 6950 \ \)

【ワンポイント解説】

発電機や電動機の問題はまず，等価回路を描くことが重要です。本問から，図1の等価回路及び図2のベクトル図を描けるようにしておきましょう。

1.同期発電機の等価回路及びベクトル図(1相分)


\[
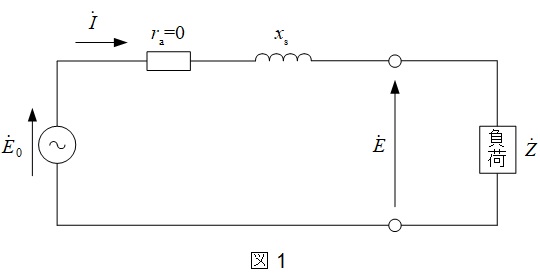
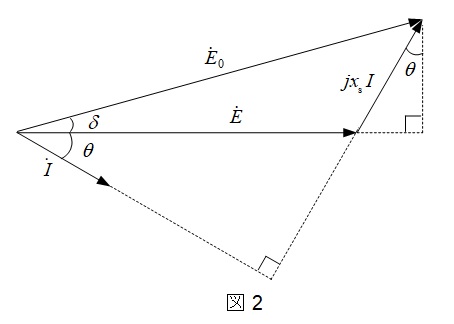
\begin{eqnarray}
&&\dot E_{0}&:&誘導起電力　&\dot E&&:&端子電圧(相電圧) \\[ 5pt ] &&\dot I&:&電機子電流　&r_{\mathrm {a}}& &:&電機子巻線抵抗 \\[ 5pt ] &&x_{\mathrm {s}}&:&同期リアクタンス　　　　　　　&\delta &&:&負荷角 \\[ 5pt ] &&\theta &:&力率角
\end{eqnarray}
\]

【解答】

(a)解答：(3)
図2より,内部起電力\( \ {\dot E}_{0} \ \)の大きさは，
\[
\begin{eqnarray}
E_{0}&=&\sqrt {\left( E+ x_{\mathrm {s}}I\sin \theta \right) ^{2} +\left( x_{\mathrm {s}}I\cos \theta \right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] で与えられる。定格相電圧の大きさ\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&\frac {6600}{\sqrt {3}} \\[ 5pt ] &≒&3811 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] となり，定格時の電機子電流\( \ I \ \)は，
\[
\begin{eqnarray}
I &=&\frac {P_{\mathrm {n}}}{\sqrt {3} V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {3300\times 10^{3}}{\sqrt {3}\times 6600} \\[ 5pt ] &≒&288.7 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] となる。また，\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.9^{2} } \\[ 5pt ] &≒&0.4359 \\[ 5pt ] \end{eqnarray}
\] となるので，各値を\( \ E_{0} \ \)の式に代入すると，
\[
\begin{eqnarray}
E_{0} &=&\sqrt {\left( E+ x_{\mathrm {s}}I\sin \theta \right) ^{2} +\left( x_{\mathrm {s}}I\cos \theta \right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( 3811+ 12.0\times 288.7 \times 0.4359 \right) ^{2} +\left( 12.0\times 288.7 \times 0.9 \right) ^{2}} \\[ 5pt ] &≒&\sqrt {5321 ^{2} +3118 ^{2}} \\[ 5pt ] &≒&6169　→　6170 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
題意より，\( \ \dot Z =13+\mathrm {j}5 \Omega \ \)であるから，図1よりの分圧の関係から，発電機端子の相電圧\(E\)は，
\[
\begin{eqnarray}
E &=&\frac {\dot Z}{\dot Z+\mathrm {j}\dot x_{\mathrm {s}}}E_{0} \\[ 5pt ] &=&\frac {13+\mathrm {j}5}{13+\mathrm {j}17}\times 6169 \\[ 5pt ] &=&\frac {\sqrt {13^{2}+5^{2}}}{\sqrt {13^{2}+17^{2}}}\times 6169 \\[ 5pt ] &=&\frac {\sqrt {194}}{\sqrt {458}}\times 6169 \\[ 5pt ] &≒&4015 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] よって，端子電圧\( \ V \ \)は，
\[
\begin{eqnarray}
V &=&\sqrt {3}E \\[ 5pt ] &=&\sqrt {3}\times 4015 \\[ 5pt ] &≒&6950 \ \mathrm {[ V ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。