Contents
【問題】
【難易度】★★★★☆(やや難しい)
均等拡散面とみなせる半径\( \ 0.3 \ \mathrm {m} \ \)の円板光源がある。円板光源の厚さは無視できるものとし,円板光源の片面のみが発光する。円板光源中心における法線方向の光度\( \ I_{0} \ \)は\( \ 2000 \ \mathrm {cd} \ \)であり,鉛直角\( \ \theta \ \)方向の光度\( \ I_{\mathrm {\theta }} \ \)は\( \ I_{\theta }=I_{0}\cos \theta \ \)で与えられる。また,円板光源の全光束\( \ F \ [\mathrm {lm}] \ \)は\( \ F=\pi I_{0} \ \)で与えられるものとする。次の(a)及び(b)の問に答えよ。
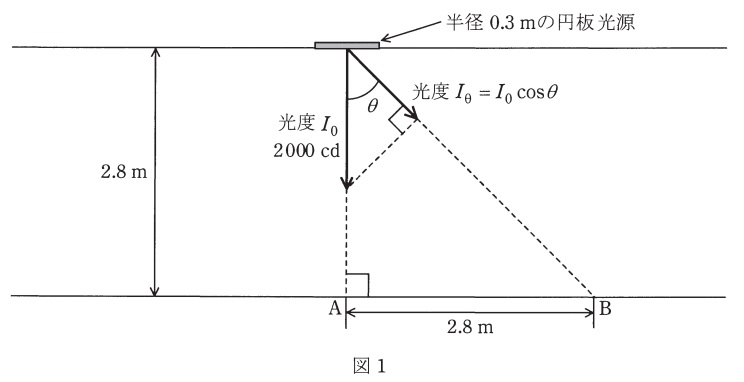
(a) 図1に示すように,この円板光源を部屋の天井面に取り付け,床面を照らす方向で部屋の照明を行った。床面B点における水平面照度の値\( \ [\mathrm {lx}] \ \)と\( \ \mathrm {B} \ \)点から円板光源の中心を見たときの輝度の値\( \ [\mathrm {cd/m^{2}}] \ \)として,最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。ただし,この部屋にはこの円板光源以外に光源はなく,天井,床,壁など,周囲からの反射光の影響はないものとする。
\[
\begin{array}{ccc}
& 水平面照度 \ \mathrm {[lx]} & 輝度 \ \mathrm {[cd / m^{2}]} \\
\hline
(1) & 64 & 5000 \\
\hline
(2) & 64 & 7080 \\
\hline
(3) & 90 & 1060 \\
\hline
(4) & 90 & 1770 \\
\hline
(5) & 255 & 7080 \\
\hline
\end{array}
\]
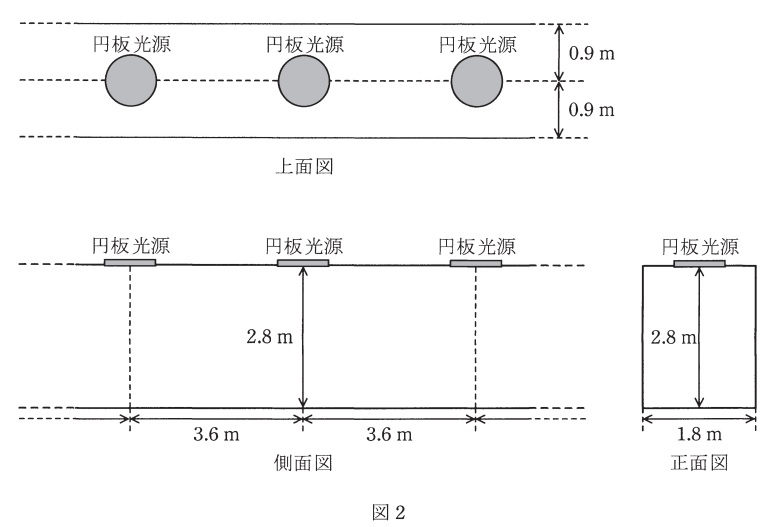
(b) 次に,図2に示すように,建物内を真っすぐ長く延びる廊下を考える。この廊下の天井面には上記円板光源が等間隔で連続的に取り付けられ,照明に供されている。廊下の長さは円板光源の取り付け間隔に比して十分大きいものとする。廊下の床面に対する照明率を\( \ 0.3 \ \),円板光源の保守率を\( \ 0.7 \ \)としたとき,廊下床面の平均照度の値\( \ \mathrm {[lx]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 102 \ \) (2) \( \ 204 \ \) (3) \( \ 262 \ \) (4) \( \ 415 \ \) (5) \( \ 2261 \ \)
【ワンポイント解説】
照明の問題は毎年必ず出題される訳ではありませんが,本問のような水平面照度に関する問題はある程度パターン化されているので,過去問の研究をすれば解けるようになります。ただし本問は例年の問題より若干複雑な問題となっています。
1.光束\( \ F \ \)
光の量で単位はルーメン\( \ [ \mathrm {lm} ] \ \)となります。電磁気で言うと磁束のようなものです。
2.照度\( \ E \ \)
均一に照射された面の明るさで,面積\( \ A \ \)に入射する光束を\( \ F \ \)とすると,
\[
\begin{eqnarray}
E&=&\frac {F}{A} \ [ \mathrm {lx}] \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.輝度\( \ L \ \)
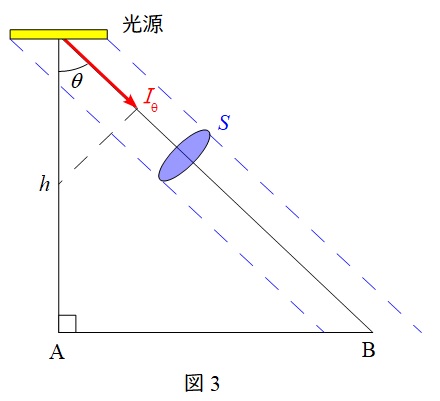
図3に示すように,\( \ \mathrm {B} \ \)点から見た輝度は\( \ \mathrm {B} \ \)点から見た光源のまぶしさを表す指標で,
\[
\begin{eqnarray}
L&=&\frac {I_{\theta }}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.逆\( \ 2 \ \)乗の法則
照度\( \ E \ \)と光度\( \ I \ \)と光源からの距離\( \ l \ \)の間に,
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ]
\end{eqnarray}
\]
が成立するという法則です。
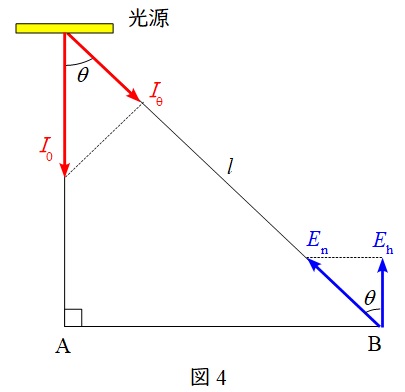
5.水平面照度
図4における\( \ E_{\mathrm {n}} \ \)を法線照度,\( \ E_{\mathrm {h}} \ \)を水平面照度と言い,以下のような関係があります。
\[
\begin{eqnarray}
E_{\mathrm {n}}&=&\frac {I_{\theta }}{l^{2}} \\[ 5pt ]
E_{\mathrm {h}}&=&E_{\mathrm {\mathrm {n}}}\cos\theta \\[ 5pt ]
&=&\frac {I_{\theta }\cos\theta }{l^{2}} \\[ 5pt ]
\end{eqnarray}
\]
6.照明率\( \ U \ \)と保守率\( \ M \ \)
照明率\( \ U \ \)は光源から出た光がどの程度床面まで到達するかを表すもので,保守率\( \ M \ \)は初期照度から劣化等でどの程度照度が低下するかを表すものです。光源から出た光束\( \ F \ \)が照射される面積を\( \ A \ \)とすると,平均照度\( \ E \ \)は,
\[
\begin{eqnarray}
E&=&\frac {FUM}{A} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(2)
図1において,照明の高さが\( \ 2.8 \ \mathrm {m} \ \)でかつ\( \ \mathrm {AB} \ \)間の距離が\( \ 2.8 \ \mathrm {m} \ \)であるから,\( \ \displaystyle \theta =\frac {\pi }{4} \ \)となり,\( \ \displaystyle \cos \theta =\frac {1}{\sqrt {2}} \ \)となる。
ここで,照明から\( \ \mathrm {B} \ \)点までの距離\( \ l \ \)とすると,逆2乗の法則から\( \ \mathrm {B} \ \)点での法線照度\( \ E_{\mathrm {n}} \ \)は,
\[
E_{\mathrm {n}}=\frac {I_{\theta }}{l^{2}}
\]
となり,水平面照度\( \ E_{\mathrm {h}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {h}} &=& E_{\mathrm {n}}\cos\theta \\[ 5pt ]
&=& \frac {I_{\theta }\cos\theta }{l^{2}} \\[ 5pt ]
&=& \frac {I_{0 }\cos^{2}\theta }{l^{2}} \\[ 5pt ]
&=& \frac {\displaystyle 2000\times \frac {1}{2}}{(2.8\times \sqrt {2})^{2}} \\[ 5pt ]
&≒& 64 \ [\mathrm {lx}]
\end{eqnarray}
\]
となる。
次に,B点から光源を見た時の輝度\( \ L \ \)を求める。\( \ \mathrm {B} \ \)点から見た光源の面積\( \ S \ \)は,
\[
\begin{eqnarray}
S&=&\pi \times 0.3^{2}\cos \theta=\frac {0.09\pi }{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「3.輝度\( \ L \ \)」より,\( \ L \ \)は,
\[
\begin{eqnarray}
L&=&\frac {I_{\theta }}{S} \\[ 5pt ]
\end{eqnarray}
\]
となり,各値を代入して整理すると,
\[
\begin{eqnarray}
L &=& \frac {I_{0 }\cos\theta }{S} \\[ 5pt ]
&=& \frac {\displaystyle 2000\times \frac {1}{\sqrt {2}} }{\displaystyle \frac {0.09\pi }{\sqrt {2}}} \\[ 5pt ]
&≒& 7074 \ [\mathrm {cd/m^{2}}]
\end{eqnarray}
\]
となる。
(b)解答:(2)
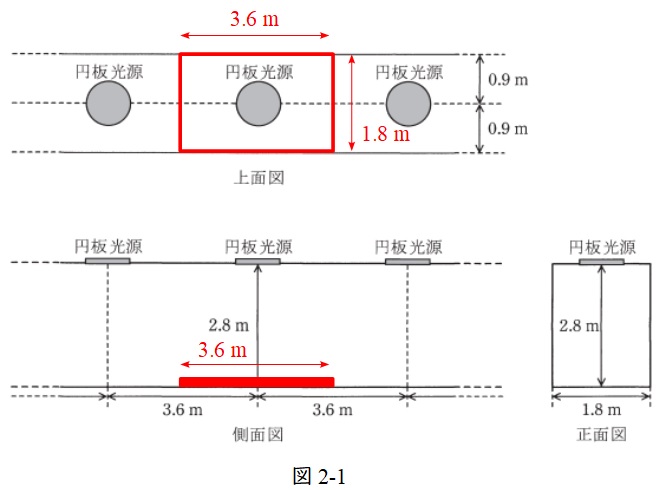
図2-1に示すように,1照明あたりの照射面積\( \ A \ \)は,
\[
\begin{eqnarray}
A&=&3.6\times 1.8 \\[ 5pt ]
&=&6.48 \ [\mathrm {m^{2}}] \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「6.照明率\( \ U \ \)と保守率\( \ M \ \)」より,平均照度\( \ E \ \)は,照明率\( \ U \ \)及び保守率\( \ M \ \)とすると,
\[
\begin{eqnarray}
E &=& \frac {FUM}{A} \\[ 5pt ]
&=& \frac {\pi I_{0}UM}{A} \\[ 5pt ]
&=& \frac {\pi \times 2000\times 0.3\times 0.7 }{6.48} \\[ 5pt ]
&≒&204 \ [\mathrm {lx}]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは