《機械》〈自動制御〉[R01:問13]周波数伝達関数に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

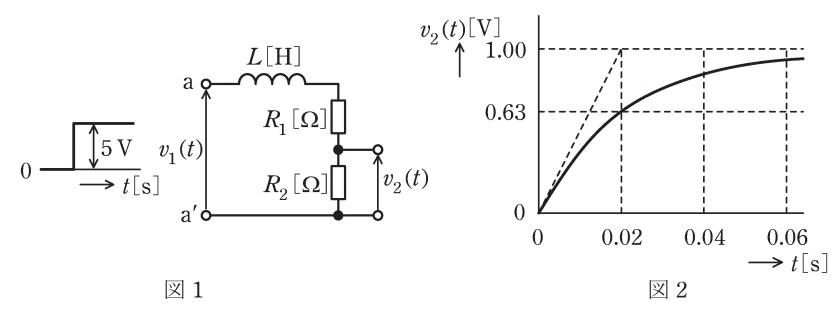
図1に示す\( \ \mathrm {R}－\mathrm {L} \ \)回路において，端子\( \ \mathrm {a}－\mathrm {a^{\prime }} \ \)間に\( \ 5 \ \mathrm {V} \ \)の階段状のステップ電圧\( \ v_{1}\left( t\right) \ \mathrm {[V]} \ \)を加えたとき，抵抗\( \ R_{2} \ \mathrm {[\Omega ]} \ \)に発生する電圧を\( \ v_{2}\left( t\right) \ \mathrm {[V]} \ \)とすると，\( \ v_{2}\left( t\right) \ \)は図2のようになった。この回路の\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，\( \ R_{2} \ \mathrm {[\Omega ]} \ \)及び\( \ L \ \mathrm {[H]} \ \)の値と，入力を\( \ v_{1}\left( t\right) \ \)，出力を\( \ v_{2}\left( t\right) \ \)としたときの周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) \ \)の式として，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& R_{1} & R_{2} & L & G\left( \mathrm {j}\omega \right) \\
\hline
(1) & 80 & 20 & 0.2 & \displaystyle \frac {0.5}{1+\mathrm {j}0.2\omega } \\
\hline
(2) & 40 & 10 & 1.0 & \displaystyle \frac {0.5}{1+\mathrm {j}0.02\omega } \\
\hline
(3) & 8 & 2 & 0.1 & \displaystyle \frac {0.2}{1+\mathrm {j}0.2\omega } \\
\hline
(4) & 4 & 1 & 0.1 & \displaystyle \frac {0.2}{1+\mathrm {j}0.02\omega } \\
\hline
(5) & 0.8 & 0.2 & 1.0 & \displaystyle \frac {0.2}{1+\mathrm {j}0.2\omega } \\
\hline
\end{array}
\]

【ワンポイント解説】

自動制御に関する問題です。解法を知らないとどうすれば良いのか全く分からないですが，解法を知っていれば比較的すんなり解ける問題となっています。少し特殊な問題ですが，回路計算にもつながる良い問題と思うので，理解しておくようにしましょう。

1.時定数\( \ T \ \)
回路の過渡現象において定常値の約\( \ 63.2 \ \mathrm {[％]} \ \)の変化になる時間を時定数と呼び，応答の速さを示す尺度となります。

①\( \ RL \ \)直列回路の時定数
\( \ RL \ \)直列回路における時定数\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&\frac {L}{R} \\[ 5pt ] \end{eqnarray}
\] となります。

②\( \ RC \ \)直列回路の時定数
\( \ RC \ \)直列回路における時定数\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&RC \\[ 5pt ] \end{eqnarray}
\] となります。

2.一次遅れ要素のステップ応答
単位ステップ応答を加えた時の伝達関数\( \ G (s) \ \)は，\( \ K \ \)を最終値，\( \ T \ \)を時定数とすると，
\[
\begin{eqnarray}
G (s) &=&\frac {K}{1+Ts} \\[ 5pt ] \end{eqnarray}
\] で与えられます。

【解答】

解答：(4)
図2より，一次遅れ要素の最終値\( \ K \ \)は，
\[
\begin{eqnarray}
K &=&\frac {v_{2}\left( \infty \right) }{v_{1}\left( \infty \right) } \\[ 5pt ] &=&\frac {1}{5} \\[ 5pt ] &=&0.2 \\[ 5pt ] \end{eqnarray}
\] となり，時定数\( \ T \ \)は\( \ 0.02 \ \)となるので，ワンポイント解説「2.一次遅れ要素のステップ応答」の通り，これを満たす\( \ G\left( \mathrm {j}\omega \right) \ \)は，
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\displaystyle \frac {0.2}{1+\mathrm {j}0.02\omega } \\[ 5pt ] \end{eqnarray}
\] と求められる。

[別解]
図1より回路に流れる電流を\( \ i \ \)とすると，回路方程式は，
\[
\begin{eqnarray}
v_{1}\left( t \right) &=&\left( R_{1}+R_{2}+\mathrm {j}\omega L\right) i \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle i=\frac {v_{2}\left( t \right) }{R_{2}} \ \)及び\( \ \displaystyle G\left( \mathrm {j}\omega \right) =\frac {v_{2}\left( t \right) }{v_{1}\left( t \right) } \ \)であるから，
\[
\begin{eqnarray}
v_{1}\left( t \right) &=&\left( R_{1}+R_{2}+\mathrm {j}\omega L\right) \frac {v_{2}\left( t \right) }{R_{2}} \\[ 5pt ] \frac {v_{2}\left( t \right) }{v_{1}\left( t \right) }&=&\frac {R_{2}}{R_{1}+R_{2}+\mathrm {j}\omega L} \\[ 5pt ] G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {R_{2}}{R_{1}+R_{2}}}{\displaystyle 1+\mathrm {j}\frac {L}{R_{1}+R_{2}}\omega } \\[ 5pt ] \end{eqnarray}
\] となる。(1)～(5)の選択肢を上式に当てはまると，
(1)
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {20}{80+20}}{\displaystyle 1+\mathrm {j}\frac {0.2}{80+20}\omega } \\[ 5pt ] &=&\frac {0.2}{\displaystyle 1+\mathrm {j}0.002\omega } \\[ 5pt ] \end{eqnarray}
\] (2)
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {10}{40+10}}{\displaystyle 1+\mathrm {j}\frac {1.0}{40+10}\omega } \\[ 5pt ] &=&\frac {0.2}{\displaystyle 1+\mathrm {j}0.02\omega } \\[ 5pt ] \end{eqnarray}
\] (3)
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {2}{8+2}}{\displaystyle 1+\mathrm {j}\frac {0.1}{8+2}\omega } \\[ 5pt ] &=&\frac {0.2}{\displaystyle 1+\mathrm {j}0.01\omega } \\[ 5pt ] \end{eqnarray}
\] (4)
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {1}{4+1}}{\displaystyle 1+\mathrm {j}\frac {0.1}{4+1}\omega } \\[ 5pt ] &=&\frac {0.2}{\displaystyle 1+\mathrm {j}0.02\omega } \\[ 5pt ] \end{eqnarray}
\] (5)
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {0.2}{0.8+0.2}}{\displaystyle 1+\mathrm {j}\frac {1}{0.8+0.2}\omega } \\[ 5pt ] &=&\frac {0.2}{\displaystyle 1+\mathrm {j}\omega } \\[ 5pt ] \end{eqnarray}
\] となり，条件を満たすのは(4)となる。