Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
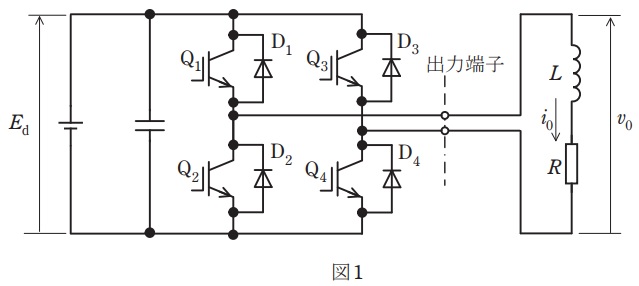
図1は,\( \ \mathrm {IGBT} \ \)を用いた単相ブリッジ接続の電圧形インバータを示す。直流電圧\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)は,一定値と見なせる。出力端子には,インダクタンス\( \ L \ \mathrm {[H]} \ \)で抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)の誘導性負荷が接続されている。この電圧形インバータの出力電圧\( \ v_{\mathrm {0}} \ \),出力電流\( \ i_{\mathrm {0}} \ \)が図2のようになった。インバータの動作モードを図2に示す①~④として本モードは周期\( \ T \ \mathrm {[s]} \ \)で繰り返されるものとする。なお,上下スイッチの短絡を防ぐデッドタイムは考慮しない。
次の(a)及び(b)の問に答えよ。
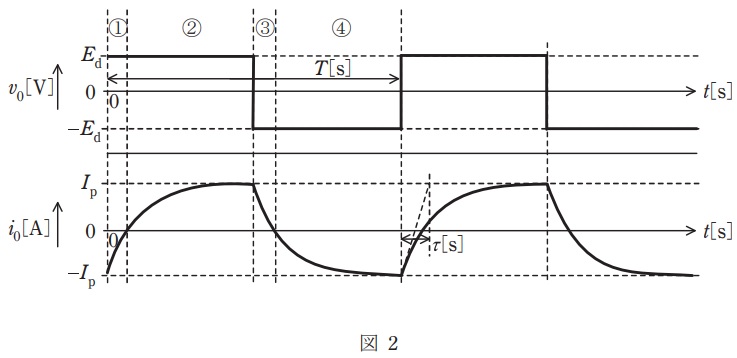
(a) 図2に示した区間①~④において電流が流れているデバイスの組合せとして正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& ① & ② & ③ & ④ \\
\hline
(1) & \mathrm {D_{2}-D_{3}} & \mathrm {Q_{2}-Q_{3}} & \mathrm {D_{1}-D_{4}} & \mathrm {Q_{1}-Q_{4}} \\
\hline
(2) & \mathrm {D_{1}-D_{4}} & \mathrm {Q_{1}-Q_{4}} & \mathrm {D_{2}-D_{3}} & \mathrm {Q_{2}-Q_{3}} \\
\hline
(3) & \mathrm {Q_{1}-Q_{4}} & \mathrm {Q_{1}-Q_{4}} & \mathrm {Q_{2}-Q_{3}} & \mathrm {Q_{2}-Q_{3}} \\
\hline
(4) & \mathrm {Q_{1}-D_{3}} & \mathrm {Q_{1}-Q_{4}} & \mathrm {Q_{2}-D_{4}} & \mathrm {Q_{2}-Q_{3}} \\
\hline
(5) & \mathrm {Q_{2}-Q_{3}} & \mathrm {Q_{2}-Q_{3}} & \mathrm {Q_{1}-Q_{4}} & \mathrm {Q_{1}-Q_{4}} \\
\hline
\end{array}
\]
(b) 電源電圧\( \ E_{\mathrm {d}} \ \)が\( \ 100 \ \mathrm {V} \ \),インダクタンス\( \ L \ \)を\( \ 2 \ \mathrm {mH} \ \)とし,抵抗\( \ R \ \)を\( \ 1 \ \mathrm {\Omega } \ \)とすると,区間①②の電流は\( \ -I_{\mathrm {p}} \ \mathrm {[A]} \ \)から\( \ I_{\mathrm {p}} \ \mathrm {[A]} \ \)まで時定数\( \ \tau \ \mathrm {[s]} \ \)で増加する。\( \ \tau \ \)に最も近い値を次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.001 \ \) (2) \( \ 0.002 \ \) (3) \( \ 0.003 \ 2 \ \) (4) \( \ 0.006 \ 3 \ \) (5) \( \ 0.02 \ \)
【ワンポイント解説】
単相ブリッジ電圧形インバータの動作に関する問題です。
令和4年度上期試験問16にも出題されていたので,十分に対策できている受験生も多かったのではないかと思います。
時定数は理論科目の過渡現象で扱う内容で,試験対策としてはまずは覚えておくのがよいかと思います。
1.単相ブリッジインバータの動作
本問の単相ブリッジインバータの動作は以下の通りとなります。各素子の役割や電流の流れを理解していると様々な問題に対応できることになります。
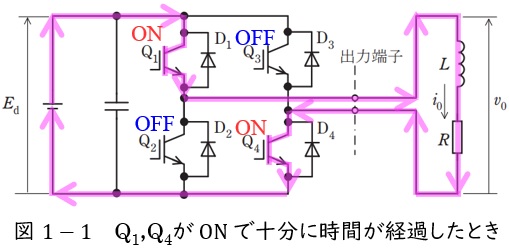
①\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
図1-1に示すように\( \ E_{\mathrm {d}} \ \)→\( \ \mathrm {Q_{1}} \ \)→\( \ L \ \)→\( \ R \ \)→\( \ \mathrm {Q_{4}} \ \)→\( \ E_{\mathrm {d}} \ \)と導通します。
図1-1より出力端子の電圧は\( \ v_{\mathrm {0}}=E_{\mathrm {d}} \ \)となり,出力電流\( \ i_{\mathrm {0}}>0 \ \)でリアクトル\( \ L \ \)にエネルギーが蓄えられます。
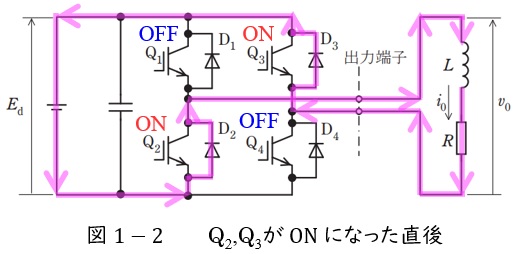
②\( \ \mathrm {Q_{2}} \ \)及び\( \ \mathrm {Q_{3}} \ \)が\( \ \mathrm {ON} \ \)になった直後
リアクトル\( \ L \ \)が電流\( \ i_{\mathrm {0}}>0 \ \)を維持しようとするので,リアクトル\( \ L \ \)に蓄えられているエネルギーが放出し,図1-2に示すように\( \ L \ \)→\( \ R \ \)→\( \ \mathrm {D_{3}} \ \)→\( \ E_{\mathrm {d}} \ \)→\( \ \mathrm {D_{2}} \ \)→\( \ L \ \)と導通します。
図1-2より出力端子の電圧は\( \ v_{\mathrm {0}}=-E_{\mathrm {d}} \ \)となり,出力電流\( \ i_{\mathrm {0}}>0 \ \)でリアクトル\( \ L \ \)のエネルギーが放出されます。
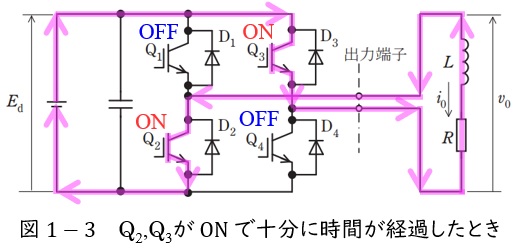
③\( \ \mathrm {Q_{2}} \ \)及び\( \ \mathrm {Q_{3}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
リアクトル\( \ L \ \)のエネルギーがなくなり,図1-3に示すように\( \ E_{\mathrm {d}} \ \)→\( \ \mathrm {Q_{3}} \ \)→\( \ R \ \)→\( \ L \ \)→\( \ \mathrm {Q_{2}} \ \)→\( \ E_{\mathrm {d}} \ \)と導通します。
図1-3より出力端子の電圧は\( \ v_{\mathrm {0}}=-E_{\mathrm {d}} \ \)となり,出力電流\( \ i_{\mathrm {0}}<0 \ \)でリアクトル\( \ L \ \)にエネルギーが蓄えられます。
④\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になった直後
リアクトル\( \ L \ \)が電流\( \ i_{\mathrm {0}}<0 \ \)を維持しようとするので,リアクトル\( \ L \ \)に蓄えられているエネルギーが放出し,図1-4に示すように\( \ L \ \)→\( \ \mathrm {D_{1}} \ \)→\( \ E_{\mathrm {d}} \ \)→\( \ \mathrm {D_{4}} \ \)→\( \ R \ \)→\( \ L \ \)と導通します。
図1-4より出力端子の電圧は\( \ v_{\mathrm {0}}=E_{\mathrm {d}} \ \)となり,出力電流\( \ i_{\mathrm {0}}<0 \ \)でリアクトル\( \ L \ \)のエネルギーが放出されます。
以降①~④を繰り返します。

2.時定数
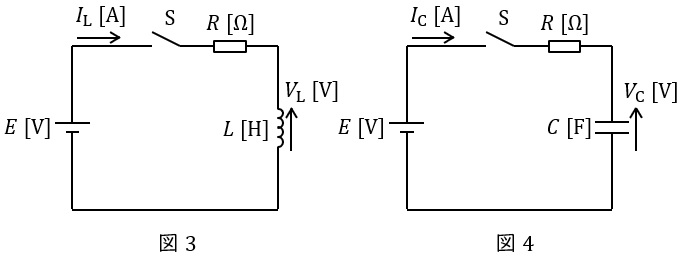
過渡現象におけるリアクトルやコンデンサの電圧の導出は微分方程式の計算を伴うため二種以上の範囲となりますが,図3や図4のような回路が与えられスイッチ\( \ \mathrm {S} \ \)を閉じたとき,図3のリアクトル電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \),図4のコンデンサ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)はそれぞれ,
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&E\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ]
I_{\mathrm {L}} &=&\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ]
V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ]
I_{\mathrm {C}} &=&\frac {E}{R}\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
で与えられ,\( \ \displaystyle t=\frac {L}{R} \ \)及び\( \ t=CR \ \)となる時間を時定数\( \ \tau \ \)と呼びます。
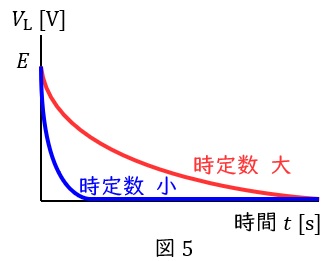
時定数\( \ \tau \ \)が大きくなると図5のように経過時間に対し,収束するまでの時間が遅くなります。
【解答】
(a)解答:(2)
①のとき
ワンポイント解説「1.単相ブリッジインバータの動作」の通り,図2の①は\( \ v_{\mathrm {0}}=E_{\mathrm {d}} \ \)で\( \ i_{\mathrm {0}}<0 \ \)であり,\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になった直後の状態である。
したがって,図1-4の状態となるため,電流が流れているデバイスは\( \ \mathrm {D_{1}-D_{4}} \ \)となる。
②のとき
ワンポイント解説「1.単相ブリッジインバータの動作」の通り,図2の②は\( \ v_{\mathrm {0}}=E_{\mathrm {d}} \ \)で\( \ i_{\mathrm {0}}>0 \ \)であり,\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になり,リアクトルのエネルギーが放出された後の状態である。
したがって,図1-1の状態となるため,電流が流れているデバイスは\( \ \mathrm {Q_{1}-Q_{4}} \ \)となる。
③のとき
ワンポイント解説「1.単相ブリッジインバータの動作」の通り,図2の③は\( \ v_{\mathrm {0}}=-E_{\mathrm {d}} \ \)で\( \ i_{\mathrm {0}}>0 \ \)であり,\( \ \mathrm {Q_{2}} \ \)及び\( \ \mathrm {Q_{3}} \ \)が\( \ \mathrm {ON} \ \)になった直後の状態である。
したがって,図1-2の状態となるため,電流が流れているデバイスは\( \ \mathrm {D_{2}-D_{3}} \ \)となる。
④のとき
ワンポイント解説「1.単相ブリッジインバータの動作」の通り,図2の④は\( \ v_{\mathrm {0}}=-E_{\mathrm {d}} \ \)で\( \ i_{\mathrm {0}}<0 \ \)であり,\( \ \mathrm {Q_{2}} \ \)及び\( \ \mathrm {Q_{3}} \ \)が\( \ \mathrm {ON} \ \)になり,リアクトルのエネルギーが放出された後の状態である。
したがって,図1-3の状態となるため,電流が流れているデバイスは\( \ \mathrm {Q_{2}-Q_{3}} \ \)となる。
(b)解答:(2)
ワンポイント解説「2.時定数」の通り,時定数\( \ \tau \ \mathrm {[s]} \ \)は,
\[
\begin{eqnarray}
\tau &=&\frac {L}{R} \\[ 5pt ]
&=&\frac {2\times 10^{-3}}{1} \\[ 5pt ]
&=&0.002 \ \mathrm {[s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは