Contents
【問題】
【難易度】★★★☆☆(普通)
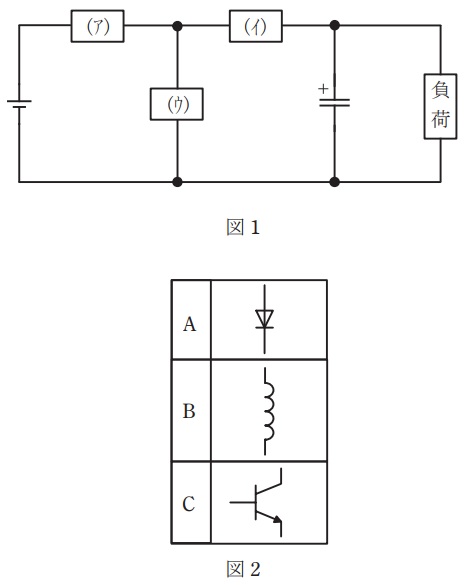
図1は直流チョッパ回路の基本構成図を示している。降圧チョッパを構成するデバイスを図 2 より選んで回路を構成したい。(ア)~(ウ)に入るデバイスの組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,図2に示す図記号の向きは任意に変更できるものとする。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & \mathrm {B} & \mathrm {A} & \mathrm {C} \\
\hline
(2) & \mathrm {B} & \mathrm {C} & \mathrm {A} \\
\hline
(3) & \mathrm {C} & \mathrm {A} & \mathrm {B} \\
\hline
(4) & \mathrm {C} & \mathrm {B} & \mathrm {A} \\
\hline
(5) & \mathrm {A} & \mathrm {B} & \mathrm {C} \\
\hline
\end{array}
\]
【ワンポイント解説】
降圧チョッパに関する問題です。
チョッパの問題としては出題のされにくい出題方式で,うろ覚えの受験生には厳しい問題であったかと思います。
各チョッパの回路は丸暗記するのではなく,動作原理をしっかりと理解した上で正答できるようにして下さい。
ただし,本問は平成17年問8からの再出題となりますので,古い過去問まで学習していれば解けた問題かと思います。
1.降圧チョッパの動作
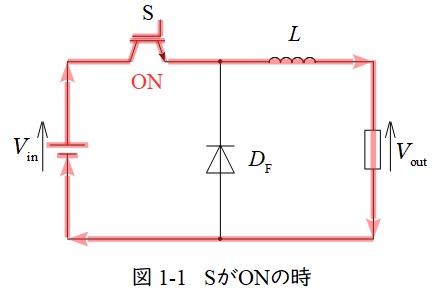
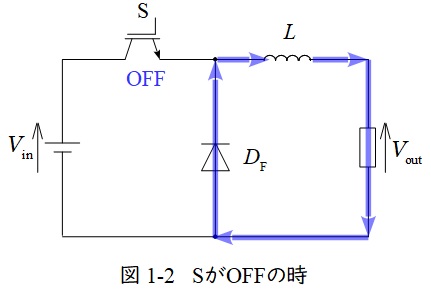
図1-1及び図1-2は降圧チョッパの例となります。
スイッチ\( \ \mathrm {S} \ \)がオンになると,図1-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り,リアクトル\( \ L \ \)側に電流が流れますが,ダイオード\( \ D_{\mathrm {F}} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると,図1-2のように電源から電流は流れず,リアクトルに蓄えられてるエネルギーから出力側と還流ダイオード\( \ D_{\mathrm {F}} \ \)に電流が流れます。
したがって降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {out}} \ \)は,スイッチのオン時間を\( \ T_{\mathrm {on}} \ \),オフ時間を\( \ T_{\mathrm {off}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。このとき,\( \ V_{\mathrm {in}} \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ]
\end{eqnarray}
\]
を通流率といいます。
2.昇圧チョッパの動作
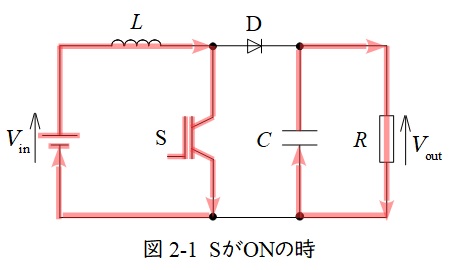
図2-1及び図2-2に昇圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時は図2-1のように導通し,電源\( \ V_{\mathrm {in}} \ \)からリアクトル\( \ L \ \)にエネルギー\( \ V_{\mathrm {in}}IT_{\mathrm {on}} \ \)が蓄えられ,出力側はコンデンサ\( \ C \ \)から電荷が供給されます。
スイッチ\( \ \mathrm {OFF} \ \)時は図2-2のように導通し,リアクトル\( \ L \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので,
\[
\begin{eqnarray}
V_{\mathrm {in}}IT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {in}}T_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ]
L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また回路方程式は,
\[
\begin{eqnarray}
V_{\mathrm {in}}+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {out}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
V_{\mathrm {in}}+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {out}} \\[ 5pt ]
V_{\mathrm {in}}+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}}&=&V_{\mathrm {out}} \\[ 5pt ]
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
となります。通流率\( \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を用いて表すと,\( \ \displaystyle 1-\gamma =\frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {1}{1-\gamma }V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
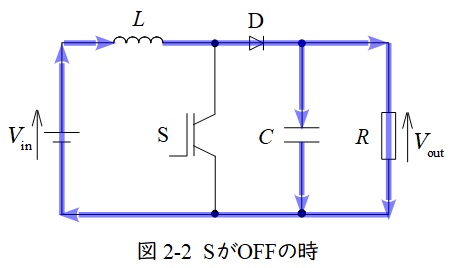
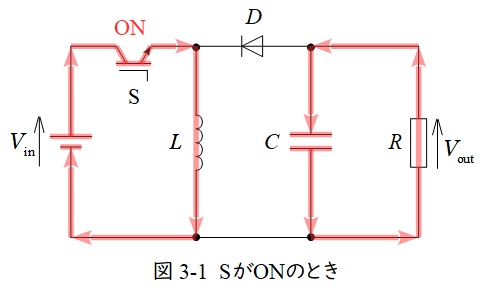
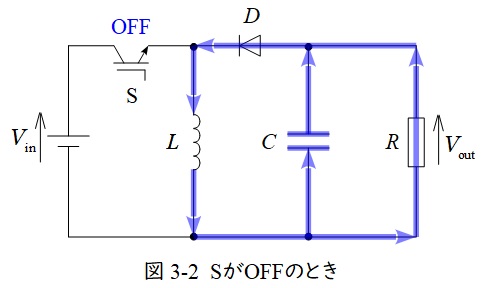
3.昇降圧チョッパの動作
図3-1及び図3-2に昇圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)がオンのとき,図3-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り,リアクトル\( \ L \ \)側にエネルギーが蓄えられますが,ダイオード\( \ D \ \)は逆向きなので電流が流れません。また,コンデンサ\( \ C \ \)に蓄えられている電荷が出力側に流れます。
スイッチ\( \ \mathrm {S} \ \)がオフになると,図3-2のように電源から電流は流れず,リアクトル\( \ L \ \)に蓄えられていたエネルギーが放出され,コンデンサ\( \ C \ \)と出力側に電流が流れます。
したがって,コンデンサ\( \ C \ \)の容量が十分に大きければ,出力電圧はほぼ一定の値となります。
定常状態においてはリアクトルに蓄えられるエネルギーと放出されるエネルギーが等しいので,スイッチ\( \ \mathrm {S} \ \)のオン時間を\( T_{\mathrm {on}} \ \),オフ時間を\( T_{\mathrm {off}} \ \),出力電圧\( \ V_{\mathrm {out}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {in}}iT_{\mathrm {on}} &=& V_{\mathrm {out}} iT_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {in}}T_{\mathrm {on}} &=&V_{\mathrm {out}} T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {out}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
となり,通流率\( \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を用いて表すと,
\[
\begin{eqnarray}
V_{\mathrm {out}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}V_{\mathrm {in}} \\[ 5pt ]
&=&\frac {\gamma }{\displaystyle 1-\gamma }V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(4)
ワンポイント解説「1.降圧チョッパの動作」の通り,(ア)がスイッチの\( \ \mathrm {C} \ \),(イ)がリアクトルの\( \ \mathrm {B} \ \),(ウ)がダイオードの\( \ \mathrm {A} \ \)となります。
ダイオードの向き等にも注意するようにして下さい。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは