Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
電気給湯器を用いて,貯湯タンクに入っている温度\( \ 20 \ \mathrm {℃} \ \),体積\( \ 0.37 \ \mathrm {m^{3}} \ \)の水を\( \ 85 \ \mathrm {℃} \ \)に加熱したい。水の比熱容量は\( \ 4.18\times 10^{3} \ \mathrm {J/\left( kg\cdot K\right) } \ \),水の密度は\( \ 1.00\times 10^{3} \ \mathrm {kg/m^{3}} \ \)であり,いずれも水の温度に関係なく一定とする。次の(a)及び(b)の問に答えよ。
(a) 貯湯タンク内の水の加熱に必要な熱エネルギー\( \ Q \ \)の値\( \ \mathrm {[MJ]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 51 \ \) (2) \( \ 101 \ \) (3) \( \ 152 \ \) (4) \( \ 202 \ \) (5) \( \ 253 \ \)
(b) 電気給湯器として\( \ \mathrm {COP} \ \)(成績係数)が\( \ 4.0 \ \)のヒートポンプユニットを用いた。この加熱に要した時間は\( \ 6 \ \)時間であった。ヒートポンプユニットの消費電力\( \ P \ \)の値\( \ \mathrm {[kW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,ヒートポンプ式電気給湯器の貯湯タンク,ヒートポンプユニット,配管などの加熱に必要な熱エネルギーは無視し,それらからの熱損失もないものとする。また,ヒートポンプユニットの消費電力及び\( \ \mathrm {COP} \ \)は,いずれも加熱の開始から終了まで一定とする。
(1) \( \ 0.96 \ \) (2) \( \ 1.06 \ \) (3) \( \ 1.16 \ \) (4) \( \ 1.26 \ \) (5) \( \ 1.36 \ \)
【ワンポイント解説】
(a)は非常に易しい問題,(b)は成績係数を理解しているかを問う問題となっています。ヒートポンプに関する問題は数年に一度出題されており,一番近い年では平成28年問17に類題が掲載されています。計算のパターンがほぼ同じなので,理解しておくと出題された時完答することも可能となります。
1.ヒートポンプの構成機器
ヒートポンプのフローを図1に示します。冷房時が青線,暖房時は赤線の流れとなります。冷房時を例に示します。
蒸発器:膨張弁からの低温低圧の液を蒸発させ気化させます。
四方弁:暖房冷房時に圧縮機に流れる媒体の向きを同じにするために向きを変えるものです。
圧縮機:蒸発器から出た低圧の蒸気を高圧蒸気にします。
凝縮器:圧縮機で高温高圧となった蒸気を凝縮し,液化させます。
膨張弁:凝縮器から出た液を膨張し,低温低圧の液にします。
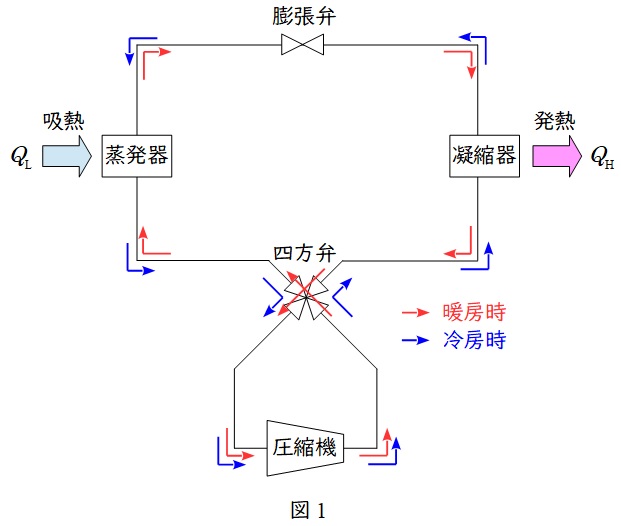
※図1において,暖房時には熱交換器である蒸発器と凝縮器の役割が逆となります。
2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))
図1において,蒸発器の吸熱量\( \ Q_{\mathrm {L}} \ \)及び圧縮機にかける仕事量\( \ W \ \)と凝縮器の放熱量\( \ Q_{\mathrm {H}} \ \)は等しいので,
\[
\begin{eqnarray}
Q_{\mathrm {H}}&=&Q_{\mathrm {L}}+W \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,冷房時と暖房時の成績係数\( \ \mathrm {{COP}_{L}} \ \),\( \ \mathrm {{COP}_{H}} \ \)は,
\[
\begin{eqnarray}
\mathrm {{COP}_{L}}&=&\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\mathrm {{COP}_{H}}&=&\frac {Q_{\mathrm {H}}}{W} \\[ 5pt ]
&=&\frac {Q_{\mathrm {L}}+W}{W} \\[ 5pt ]
&=&1+\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(2)
加熱に必要なエネルギー\( \ Q \ \)は,質量\( \ m \ \),比熱容量\( \ c \ \),温度差\( \ \Delta T \ \)とすると
\[
\begin{eqnarray}
Q &=&mc \Delta T \\[ 5pt ]
\end{eqnarray}
\]
である。ここで,体積\( \ 0.37 \ \mathrm {[m^{3}]} \ \)の水の質量\( \ m \ \)は,水の密度が\( \ 1.00\times 10^{3} \ \mathrm {kg/m^{3}} \ \)であるから,
\[
\begin{eqnarray}
m &=&0.37\times 1.00\times 10^{3} \\[ 5pt ]
&=&370 \ \mathrm {[kg]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,加熱に必要なエネルギー\( \ Q \ \)は,
\[
\begin{eqnarray}
Q &=&mc \Delta T \\[ 5pt ]
&=&370\times 4.18\times 10^{3}\times \left( 85-20\right) \\[ 5pt ]
&≒&100500000 \ \mathrm {[J]} → 101 \ \mathrm {[MJ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
ワンポイント解説「2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))」の通り,暖房時の成績係数\( \ \mathrm {COP} \ \)は,
\[
\begin{eqnarray}
\mathrm {COP}&=&\frac {Q}{W} \\[ 5pt ]
\end{eqnarray}
\]
であるから,電気給湯器に要した仕事量\( \ W \ \)は,
\[
\begin{eqnarray}
W&=&\frac {Q}{\mathrm {COP}} \\[ 5pt ]
&=&\frac {100500000}{4} \\[ 5pt ]
&≒&25130000 \ \mathrm {[J]} → 25130 \ \mathrm {[kJ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,この加熱に要した時間は\( \ 6 \ \)時間であったので,ヒートポンプユニットの消費電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {W}{6\times 3600} \\[ 5pt ]
&=&\frac {25130}{6\times 3600} \\[ 5pt ]
&≒&1.16 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは