《機械》〈電動機応用〉[R4上:問11]ロープ式エレベータに必要な電動機の出力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

かごの質量が\( \ 250 \ \mathrm {kg} \ \)，定格積載質量が\( \ 1 \ 500 \ \mathrm {kg} \ \)のロープ式エレベータにおいて，釣合いおもりの質量は，かごの質量に定格積載質量の\( \ 40 \ \mathrm {％} \ \)を加えた値とした。このエレベータで，定格積載質量を搭載したかごを一定速度\( \ 100 \ \mathrm {m / min} \ \)で上昇させるときに用いる電動機の出力の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，機械効率は\( \ 75 \ \mathrm {％} \ \)，加減速に要する動力及びロープの質量は無視するものとする。

　(1)　\( \ 2.00 \ \)　　(2)　\( \ 14.7 \ \)　　(3)　\( \ 19.6 \ \)　　(4)　\( \ 120 \ \)　　(5)　\( \ 1 \ 180 \ \)

【ワンポイント解説】

エレベータの上昇に必要な動力に関する問題です。
典型的な電動機応用の問題で特別易しい問題ではありませんが，類題が令和元年問１１に出題されていたので，正答率は高かったと予想されます。
本問では重力加速度は与えられていませんが，重力加速度\( \ g=9.8 \ \mathrm {m / s^{2}} \ \)は基本として覚えておきましょう。

1.動力\( \ P \ \mathrm {[W]} \ \)と力\( \ F \ \mathrm {[N]} \ \)の関係
仕事の定義より，力\( \ F \ \mathrm {[N]} \ \)で\( \ l \ \mathrm {[m]} \ \)運ぶのに必要な仕事量\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=& Fl \\[ 5pt ] \end{eqnarray}
\] であり，単位時間当たりの仕事量が動力\( \ P \ \mathrm {[W]} \ \)であるから，一定の動力で\( \ W \ \mathrm {[J]} \ \)の仕事をするのに\( \ t \ \mathrm {[s]} \ \)かかったとすると，
\[
\begin{eqnarray}
P &=& \frac {Fl}{t} \\[ 5pt ] \end{eqnarray}
\] となります。上式において\( \ \displaystyle \frac {l}{t} \ \)は速度\( \ v \ \mathrm {[m / s]} \ \)に等しいので，
\[
\begin{eqnarray}
P &=& Fv \\[ 5pt ] \end{eqnarray}
\] となります。この式は公式として覚えておきましょう。

【解答】

解答：(3)
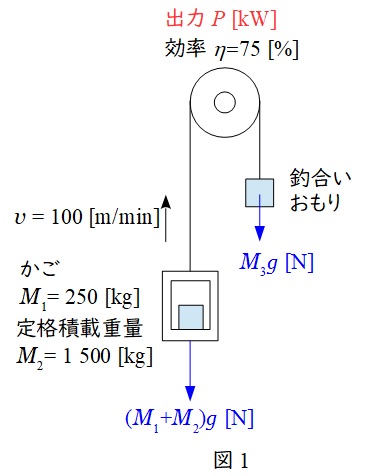
問題文に沿って図を描くと図1のようになる。
釣合いおもりの質量\( \ M_{3} \ \mathrm {[kg]} \ \)は，かごの質量\( \ M_{1}=250 \ \mathrm {[kg]} \ \)に定格積載質量\( \ M_{2}=1 \ 500 \ \mathrm {[kg]} \ \)の\( \ 40 \ \mathrm {％} \ \)を加えた値であるから，
\[
\begin{eqnarray}
M_{3} &=& M_{1}+0.4M_{2} \\[ 5pt ] &=& 250+0.4\times 1 \ 500 \\[ 5pt ] &=& 850 \ \mathrm {[kg]} \\[ 5pt ] \end{eqnarray}
\] となるので，上昇させるのに必要な力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=& \left( M_{1}+M_{2}-M_{3}\right) g \\[ 5pt ] &=& \left( 250 +1 \ 500-850\right) \times 9.8 \\[ 5pt ] &=& 8 \ 820 \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となる。電動機の出力\( \ P \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.動力\( \ P \ \mathrm {[W]} \ \)と力\( \ F \ \mathrm {[N]} \ \)の関係」より，
\[
\begin{eqnarray}
P\eta &=& Fv \\[ 5pt ] P\times 0.75 &=& 8 \ 820\times \frac {100}{60} \\[ 5pt ] P &=& 8 \ 820\times \frac {100}{60}\times \frac {1}{0.75} \\[ 5pt ] &=& 19 \ 600 \ \mathrm {[W]}　→　19.6 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。