《機械》〈回転機〉[R4上:問5]三相同期発電機の短絡比の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格出力\( \ 1 \ 500 \ \mathrm {kV\cdot A} \ \)，定格電圧\( \ 3 \ 300 \ \mathrm {V} \ \)の三相同期発電機がある。無負荷時に定格電圧となる界磁電流に対する三相短絡電流(持続短絡電流)は，\( \ 310 \ \mathrm {A} \ \)であった。この同期発電機の短絡比の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.488 \ \)　　(2)　\( \ 0.847 \ \)　　(3)　\( \ 1.18 \ \)　　(4)　\( \ 1.47 \ \)　　(5)　\( \ 2.05 \ \)

【ワンポイント解説】

短絡比の導出に関する問題です。
短絡比は定義なので，ある程度覚えるしかありません。
本問は短絡比の定義を理解する上ではとても良い問題と思いますので，必ず習得するようにしましょう。

1.同期発電機の無負荷飽和曲線と三相短絡曲線
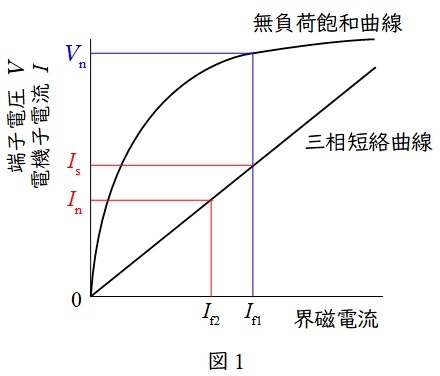
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
本問の三相同期発電機の定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，定格出力\( \ P_{\mathrm {n}}=1 \ 500 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ V_{\mathrm {n}}=3 \ 300 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
P_{\mathrm {n}} &=& \sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \\[ 5pt ] I_{\mathrm {n}} &=& \frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {1 \ 500\times 10^{3}}{\sqrt {3}\times 3 \ 300} \\[ 5pt ] &≒&262.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。これより短絡比\( \ K \ \)は，三相短絡電流\( \ I_{\mathrm {s}}=310 \ \mathrm {[A]} \ \)であるから，ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {310}{262.4} \\[ 5pt ] &≒&1.18 \\[ 5pt ] \end{eqnarray}
\] と求められる。