《機械》〈電動機応用〉[R4下:問11]水をくみ上げるために必要な電動機の入力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電動機で駆動するポンプを用いて，毎時\( \ 80 \ \mathrm {m^{3}} \ \)の水をパイプへ通して揚程\( \ 40 \ \mathrm {m} \ \)の高さに持ち上げる。ポンプの効率は\( \ 72 \ \mathrm {％} \ \)，電動機の効率は\( \ 93 \ \mathrm {％} \ \)で，パイプの損失水頭は\( \ 0.4 \ \mathrm {m} \ \)であり，他の損失水頭は無視できるものとする。このとき必要な電動機入力\( \ \mathrm {[kW]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，水の密度は\( \ 1.00\times 10^{3} \ \mathrm {kg / m^{3}} \ \)，重力加速度は\( \ 9.8 \ \mathrm {m / s^{2}} \ \)とする。

　(1)　\( \ 0.013 \ \)　　(2)　\( \ 0.787 \ \)　　(3)　\( \ 4.83 \ \)　　(4)　\( \ 13.1 \ \)　　(5)　\( \ 80.4 \ \)

【ワンポイント解説】

電動機で駆動するポンプを用いて水をくみ上げる問題ですが，内容は水力発電の揚水発電と同じです。
揚水発電所の公式をしっかりと思い出し，正答を導き出せるようにしましょう。

1.揚水発電所の諸公式
揚水発電で使用される諸公式は以下の通りです。本問で使用しない公式も覚えておくようにしましょう。

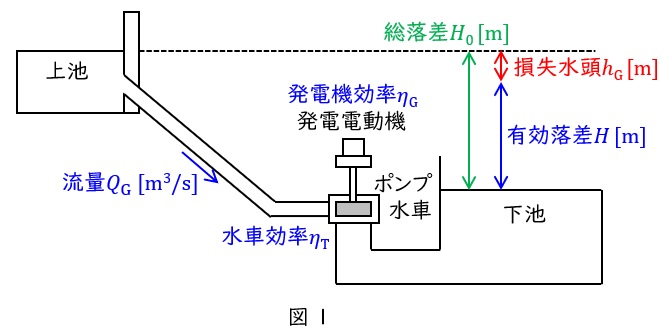
①発電電力
有効落差　：\( \ H=H_{0}-h_{\mathrm {G}} \ \mathrm {[ m ] } \ \)
発電機出力：\( \ P_{\mathrm {G}}=9.8Q_{\mathrm {G}}H\eta _{\mathrm {T}}\eta _{\mathrm {G}} \ \mathrm {[ kW ] } \ \)
総発電量　：\( \ W_{\mathrm {G}}=P_{\mathrm {G}}T_{\mathrm {G}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {G}} \ \)は発電時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {G}} \ \)は発電時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {T}} \ \)は水車効率，\( \ \eta _{\mathrm {G}} \ \)は発電機効率，\( \ T_{\mathrm {G}} \ \)は発電時間\( \ \mathrm {[h]} \ \)

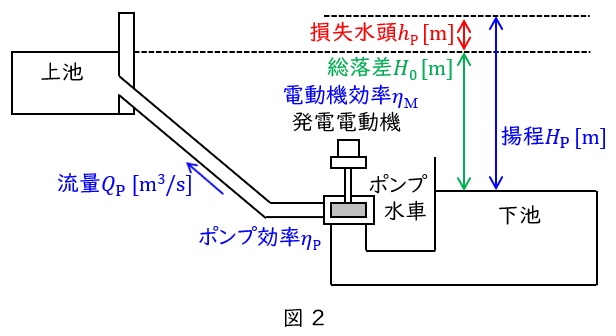
②揚水動力
必要揚程　：\( \ \displaystyle H_{\mathrm {P}}=H_{0}+h_{\mathrm {P}} \ \mathrm {[ m ] } \ \)
所要動力　：\( \ \displaystyle P_{\mathrm {M}}=\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \ \mathrm {[ kW ] } \ \)
所要電力量：\( \ W_{\mathrm {M}}=P_{\mathrm {M}}T_{\mathrm {M}} \ \mathrm {[ kW\cdot h ] } \ \)

ただし，\( \ H_{0} \ \)は総落差\( \ \mathrm {[m]} \ \)，\( \ h_{\mathrm {P}} \ \)は揚水時の損失水頭\( \ \mathrm {[m]} \ \)，\( \ Q_{\mathrm {P}} \ \)は揚水時の流量\( \ \mathrm {[m^{3} / s]} \ \)，\( \ \eta _{\mathrm {P}} \ \)はポンプ効率，\( \ \eta _{\mathrm {M}} \ \)は電動機効率，\( \ T_{\mathrm {M}} \ \)は揚水時間\( \ \mathrm {[h]} \ \)

③揚水総合効率
\[
\begin{eqnarray}
\eta &=&\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}}\times 100\mathrm {[ ％ ] } \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
パイプに通す水の流量\( \ Q \ \mathrm {[m^{3} / s]} \ \)は，
\[
\begin{eqnarray}
Q &=&\frac {80}{3 \ 600} \\[ 5pt ] &≒&0.02222 \ \mathrm {[m^{3} / s]} \\[ 5pt ] \end{eqnarray}
\] であり，必要揚程\( \ H_{\mathrm {P}} \ \mathrm {[m]} \ \)は，
\[
\begin{eqnarray}
H_{\mathrm {P}} &=&40+0.4 \\[ 5pt ] &≒&40.4 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] である。よって，ポンプの効率\( \ \eta _{\mathrm {P}}=0.72 \ \)，電動機の効率\( \ \eta _{\mathrm {M}}=0.93 \ \)であることから，必要な電動機入力\( \ \displaystyle P_{\mathrm {M}} \ \mathrm {[ kW ] } \ \)は，ワンポイント解説「1.揚水発電所の諸公式」の通り，
\[
\begin{eqnarray}
P_{\mathrm {M}}&=&\frac { 9.8QH_{\mathrm {P}}}{\eta _{\mathrm {P}}\eta _{\mathrm {M}} } \\[ 5pt ] &=&\frac { 9.8\times 0.02222 \times 40.4}{0.72\times 0.93} \\[ 5pt ] &≒&13.1 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。