《機械》〈同期機〉[R06下:問6]三相同期発電機の三相短絡電流を流すのに必要な界磁電流に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

定格出力\( \ 11 \ 000 \ \mathrm {kV\cdot A} \ \)，定格電圧\( \ 6 \ 600 \ \mathrm {V} \ \)の三相同期発電機がある。三相短絡電流\( \ 750 \ \mathrm {A} \ \)を流すのに必要な界磁電流が\( \ 54 \ \mathrm {A} \ \)である場合，この発電機の定格電流に等しい三相短絡電流を流すのに必要な界磁電流\( \ \mathrm {[A]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 69 \ \)　　(2)　\( \ 96 \ \)　　(3)　\( \ 120 \ \)　　(4)　\( \ 208 \ \)　　(5)　\( \ 289 \ \)

【ワンポイント解説】

定格電流に等しい三相短絡電流を流すのに必要な界磁電流を求める問題です。
問題文を見て，無負荷飽和曲線と三相短絡曲線を描く必要があることを判断できることが重要です。
平成29年問5に類題が出題されており，それより幾分易しめの問題となっていますので，多くの受験生が正答したと考えられます。

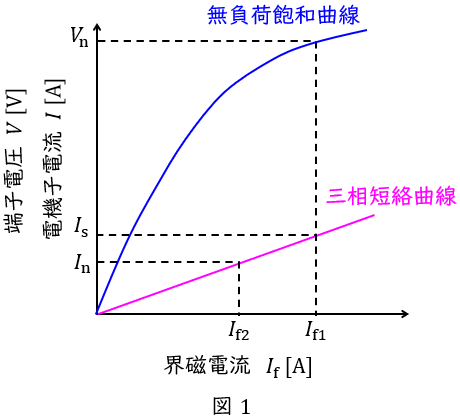
1.同期発電機の無負荷飽和曲線と三相短絡曲線
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷飽和曲線は定格速度で無負荷で運転したときの界磁電流と端子電圧の関係，三相短絡曲線は電機子巻線の三相の出力端子を短絡し定格速度で運転したときの界磁電流と三相短絡電流の関係，を表したものです。
図中の\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)は定格電圧，\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は定格電流，三相短絡曲線は曲線ですが，ほぼ比例の直線と近似できます。
この時，\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は定格電圧時の三相短絡電流であり，短絡比\( \ K \ \)は，
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}}=\frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
定格出力\( \ P_{\mathrm {n}}=11 \ 000 \ \mathrm {[kV\cdot A]} \ \)，定格電圧\( \ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ \)なので，定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=& \frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=& \frac {11 \ 000\times 10^{3}}{\sqrt {3}\times 6 \ 600} \\[ 5pt ] &≒& 962.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，三相短絡電流\( \ I_{\mathrm {s}}=750 \ \mathrm {[A]} \ \)を流すのに必要な界磁電流が\( \ I_{\mathrm {f}}=54 \ \mathrm {[A]} \ \)であるから，定格電流\( \ I_{\mathrm {n}}=962.2 \ \mathrm {[A]} \ \)を流すのに必要な界磁電流\( \ I_{\mathrm {f}}^{\prime } \ \mathrm {[A]} \ \)は，ワンポイント解説「1.同期発電機の無負荷飽和曲線と三相短絡曲線」の通り，
\[
\begin{eqnarray}
I_{\mathrm {f}}^{\prime }&=& \frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}I_{\mathrm {f}} \\[ 5pt ] &=& \frac {962.3}{750}\times 54 \\[ 5pt ] &≒& 69.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。