Contents
【問題】
【難易度】★★★★☆(やや難しい)
定格出力\( \ 10 \ \mathrm {MV\cdot A} \ \),定格電圧\( \ 6.6 \ \mathrm {kV} \ \),百分率同期インピーダンス\( \ 80 \ % \ \)の三相同期発電機がある。三相短絡電流\( \ 700 \ \mathrm {A} \ \)を流すのに必要な界磁電流が\( \ 50 \ \mathrm {A} \ \)である場合,この発電機の定格電圧に等しい無負荷端子電圧を発生させるのに必要な界磁電流の値\( \ [\mathrm {A}] \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,百分率同期インピーダンスの抵抗分は無視できるものとする。
(1) \(50.0\) (2) \(62.5\) (3) \(78.1\) (4) \(86.6\) (5) \(135.3\)
【ワンポイント解説】
同期発電機の特性曲線をよく理解していて,かつ百分率同期インピーダンスの計算を理解していないと解けない問題です。若干難しめの問題ですが,電験らしいハイレベルな良問であると思います。
1.同期発電機の特性曲線
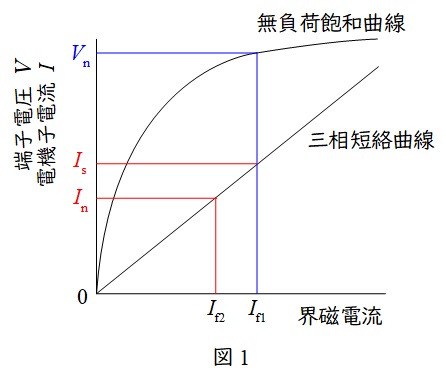
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。図中の\( \ V_{\mathrm {n}} \ \)は定格電圧,\( \ I_{\mathrm {n}} \ \)は定格電流,三相短絡曲線は曲線ですが,ほぼ比例の直線と近似できます。
この時,短絡比\( \ K \ \)は,
\[
\begin{eqnarray}
K &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.百分率同期インピーダンス\( \ %Z \ \)
図1において同期インピーダンス\( \ Z \ \)と百分率同期インピーダンス\( \ %Z \ \)は次式のように求められます。
\[
\begin{eqnarray}
Z&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{I_{\mathrm {s}}}&=&\frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
%Z &=& \frac {Z}{Z_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=& \frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 \\[ 5pt ]
&=& \frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}}I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 \\[ 5pt ]
&=& \frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}\times 100 \\[ 5pt ]
&=& \frac {1}{K}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
【解答】
解答:(3)
定格出力\( \ P_{\mathrm {n}}=10 \ \mathrm {MV\cdot A} \ \),定格電圧\( \ V_{\mathrm {n}}=6.6 \ \mathrm {kV} \ \)であるから,定格電流\( \ I_{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{\sqrt {3}\times 6.6\times 10^{3}} \\[ 5pt ]
&≒&875 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.百分率同期インピーダンス\( \ %Z \ \)」より,百分率同期インピーダンス\( \ %Z \ \),三相短絡電流\( \ I_{\mathrm {s}} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {I_{\mathrm {n}}}{I_{\mathrm {s}}}\times 100 \\[ 5pt ]
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{%Z}\times 100 \\[ 5pt ]
&=&\frac {875}{80}\times 100 \\[ 5pt ]
&≒&1094 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。図1の通り,三相短絡曲線はほぼ比例の関係があるから,定格電圧に等しい無負荷端子電圧を発生させるのに必要な界磁電流を\( \ I_{\mathrm {f1}} \ \)とすると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {s}}}{I_{\mathrm {f1}}}&=&\frac {700}{50} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ I_{\mathrm {s}}=1094 \ \mathrm {[A]} \ \)を代入すると,
\[
\begin{eqnarray}
\frac {1094}{I_{\mathrm {f1}}}&=&\frac {700}{50} \\[ 5pt ]
I_{\mathrm {f1}} &=& \frac {50\times 1094}{700} \\[ 5pt ]
&≒& 78.1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。





















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは