《理論》〈電気回路〉[H18:問10]RC回路のスイッチを切り換えた後の時定数に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

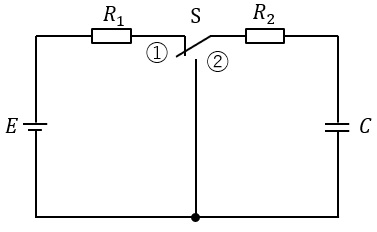
図のような回路において，スイッチ\( \ \mathrm {S} \ \)を①側に閉じて，回路が定常状態に達した後で，スイッチ\( \ \mathrm {S} \ \)を切り換え②側に閉じた。スイッチ\( \ \mathrm {S} \ \)，抵抗\( \ R_{2} \ \)及びコンデンサ\( \ C \ \)からなる閉回路の時定数の値として，正しいのは次のうちどれか。

ただし，\( \ R_{1}=300 \ \mathrm {[\Omega ]} \ \)，抵抗\( \ R_{2}=100 \ \mathrm {[\Omega ]} \ \)，コンデンサ\( \ C \ \)の静電容量\( \ =20 \ \mathrm {[\mu F]} \ \)，直流電圧\( \ E=10 \ \mathrm {[V]} \ \)とする。

　(1)　\( \ 0.05 \ \mathrm {[\mu s]} \ \)　　(2)　\( \ 0.2 \ \mathrm {[\mu s]} \ \)　　(3)　\( \ 1.5 \ \mathrm {[ms]} \ \)　　(4)　\( \ 2.0 \ \mathrm {[ms]} \ \)　　(5)　\( \ 8.0 \ \mathrm {[ms]} \ \)

【ワンポイント解説】

\( \ RC \ \)回路の時定数を求める問題です。
スイッチを①にしたときと②に切り換えた後に回路内の電流がどのようになるかをイメージし，時定数の公式に数値をあてはめていきます。
不要な情報に惑わされないことが重要です。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

3.時定数
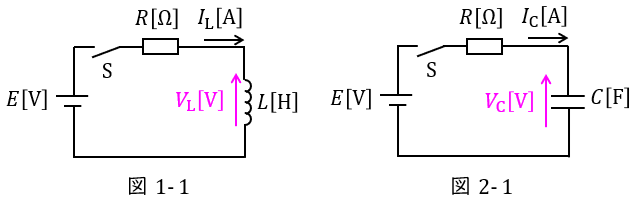
過渡現象におけるリアクトルやコンデンサの電圧の導出は微分方程式の計算を伴うため二種以上の範囲となりますが，図1-1や図2-1のような回路が与えられると，図1-1のリアクトル電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)，図2-1のコンデンサ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)はそれぞれ，
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&E\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ] I_{\mathrm {L}} &=&\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ] V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ] I_{\mathrm {C}} &=&\frac {E}{R}\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ] \end{eqnarray}
\] で与えられ，\( \ \displaystyle t=\frac {L}{R} \ \)及び\( \ t=CR \ \)となる時間を時定数\( \ \tau \ \)と呼びます。

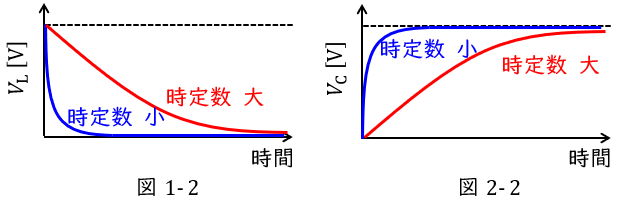
時定数\( \ \tau \ \)が大きくなると図1-2及び図2-2のように経過時間に対し，収束するまでの時間が遅くなります。

【解答】

解答：(4)
スイッチ\( \ \mathrm {S} \ \)を①側に閉じて，コンデンサ\( \ C \ \)に電荷を蓄えた後，スイッチ\( \ \mathrm {S} \ \)②側に切り換えると，電流は図3のように流れる。
したがって，このときの時定数\( \ \tau \ \mathrm {[ms]} \ \)は，ワンポイント解説「3.時定数」の通り，
\[
\begin{eqnarray}
\tau &=&CR_{2} \\[ 5pt ] &=&20\times 10^{-6}\times 100 \\[ 5pt ] &=&2.0\times 10^{-3} \ \mathrm {[s]}　→　2.0 \ \mathrm {[ms]} \\[ 5pt ] \end{eqnarray}
\] と求められる。