《理論》〈電気回路〉[H30:問15]三相交流回路の消費電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {b}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {c}} \ \mathrm {[V]} \ \)をもつ三つの定電圧源に，スイッチ\( \ \mathrm {S}_{1}\)，\( \ \mathrm {S}_{2}\)，\( \ R_{1}=10 \ \Omega \ \)及び\( \ R_{2}=20 \ \Omega \ \)の抵抗を接続した交流回路がある。次の(a)及び(b)の問に答えよ。

ただし，\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {b}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {c}} \ \mathrm {[V]} \ \)の正の向きはそれぞれ図の矢印のようにとり，これらの実効値は\( \ 100 \ \mathrm {V} \ \)，位相は\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {b}} \ \mathrm {[V]} \ \)，\( \ {\dot E}_{\mathrm {c}} \ \mathrm {[V]} \ \)の順に\(\displaystyle \frac {2}{3}\pi \ \mathrm {[rad]}\)ずつ遅れているものとする。

(a)　スイッチ\( \ \mathrm {S}_{2} \ \)を開いた状態でスイッチ\( \ \mathrm {S}_{1} \ \)を閉じたとき，\( \ R_{1} \ [\Omega ] \ \)の抵抗に流れる電流\( \ {\dot I}_{1} \ \)の実効値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0\)　　(2)　\(5.77\)　　(3)　\(10.0\)　　(4)　\(17.3\)　　(5)　\(20.0\)

(b)　スイッチ\( \ \mathrm {S}_{1} \ \)を開いた状態でスイッチ\( \ \mathrm {S}_{2} \ \)を閉じたとき，\( \ R_{2} \ [\Omega ] \ \)の抵抗で消費される電力の値\( \ \mathrm {[W]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0\)　　(2)　\(500\)　　(3)　\(1500\)　　(4)　\(2000\)　　(5)　\(4500\)

【ワンポイント解説】

三相交流回路は毎年のように\(\mathrm {B}\)問題で出題され，苦手としている受験生も多いので，合否の明暗を分ける内容となります。三相交流回路の基本はベクトル図を描くことであり，本問はそれが描ければ比較的容易に解くことができるので，三相交流回路としては易しめな問題となると思います。

1.抵抗での消費電力
\( \ R \ [\Omega ] \ \)の抵抗に電流\( \ \dot I \ \mathrm {[A]} \ \)が流れた時の消費電力\(\ P \ \mathrm {[W]} \ \)の大きさは，
\[
\begin{eqnarray}
P &=&R \left| \dot I \right| ^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(4)
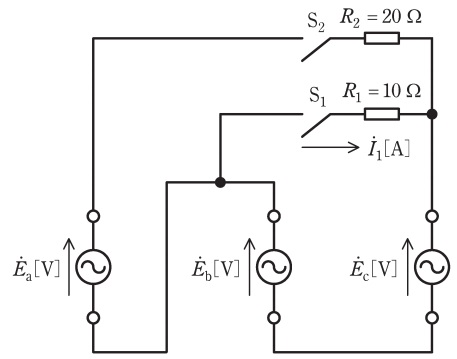
題意の条件において，\( \ R_{1} \ \)にかかる電圧は，\( {\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}\)であり，ベクトル図を描くと図1のようになる。これより，\( \left| {\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}\right| = 100\sqrt {3} \ \mathrm {[V]} \ \)であることが分かる。キルヒホッフの法則より，\( \ R_{1} \ \)の抵抗に流れる電流\( \ {\dot I}_{1} \ \)の大きさは，
\[
\begin{eqnarray}
\left| {\dot I}_{1} \right| &=&\left|\frac { {\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}}{R_{1}}\right| \\[ 5pt ] &=&\frac {100\sqrt {3}}{10} \\[ 5pt ] &≒&17.3 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

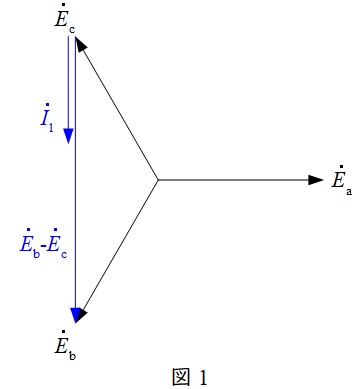
(b)解答：(4)
題意の条件において，\( \ R_{2} \ \)にかかる電圧は，\( {\dot E}_{\mathrm {a}}+{\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}\)であり，ベクトル図を描くと図2のようになる。これより，\( \left| {\dot E}_{\mathrm {a}}+{\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}\right| = \left| -2 {\dot E}_{\mathrm {c}}\right| =200 \ \mathrm {[V]} \ \)であることが分かる。キルヒホッフの法則より，\( \ R_{2} \ \)の抵抗に流れる電流\( \ {\dot I}_{2} \ \)の大きさは，
\[
\begin{eqnarray}
\left| {\dot I}_{2} \right| &=&\left|\frac {{\dot E}_{\mathrm {a}}+{\dot E}_{\mathrm {b}} – {\dot E}_{\mathrm {c}}}{R_{2}}\right| \\[ 5pt ] &=&\left|\frac {-2 {\dot E}_{\mathrm {c}}}{R_{2}}\right| \\[ 5pt ] &=&\frac {200}{20} \\[ 5pt ] &=&10 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。ワンポイント解説「1.抵抗での消費電力」より，\( \ R_{2} \ \)の抵抗で消費される電力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2} &=&R_{2}\left| {\dot I}_{2} \right| ^{2} \\[ 5pt ] &=&20\times 10^{2} \\[ 5pt ] &=&2000 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。