《理論》〈電磁気〉[H19:問4]直列，並列接続されたコンデンサの静電エネルギーの比較に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

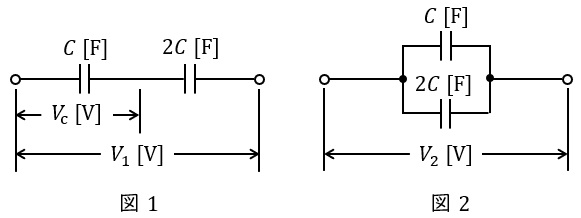
静電容量が\( \ C \ \mathrm {[F]} \ \)と\( \ 2C \ \mathrm {[F]} \ \)の二つのコンデンサを図1，図2のように直列，並列に接続し，それぞれに\( \ V_{1} \ \mathrm {[V]} \ \)，\( \ V_{2} \ \mathrm {[V]} \ \)の直流電圧を加えたところ，両図の回路に蓄えられている総静電エネルギーが等しくなった。この場合，図1の\( \ C \ \mathrm {[F]} \ \)のコンデンサの端子間の電圧を\( \ V_{c} \ \mathrm {[V]} \ \)としたとき，電圧比\( \ \displaystyle \left| \frac {V_{c}}{V_{2}}\right| \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle \frac {\sqrt {2}}{9} \ \)　　(2)　\( \ \displaystyle \frac {2\sqrt {2}}{9} \ \)　　(3)　\( \ \displaystyle \frac {1}{\sqrt {2}} \ \)　　(4)　\( \ \sqrt {2} \ \)　　(5)　\( \ 3.0 \ \)　　

【ワンポイント解説】

コンデンサに蓄えられている静電エネルギーからコンデンサに加わる電圧の比を求める問題です。
なかなか最初はゴールまでの道筋が見つからないかもしれません。その場合はまず求められるものを求めていく，例えば本問であれば合成静電容量から求めていくようにして下さい。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)のコンデンサがある場合，直並列の合成静電容量\( \ C \ \mathrm {[F]} \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\] ②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] 整理すると，
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

3.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)及びコンデンサに加わる電圧\( \ V \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
図1及び図2の回路の合成静電容量\( \ C_{1} \ \mathrm {[F]} \ \)及び\( \ C_{2} \ \mathrm {[F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C_{1}&=&\frac {C\cdot 2C}{C+ 2C} \\[ 5pt ] &=&\frac {2}{3}C \ \mathrm {[F]} \\[ 5pt ] C_{2}&=&C+ 2C \\[ 5pt ] &=&3C \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] であり，回路に蓄えられている静電エネルギーが等しいから，ワンポイント解説「3.コンデンサの静電エネルギー\( \ W \ \)」の通り，
\[
\begin{eqnarray}
\frac {1}{2}C_{1}{V_{1}}^{2}&=&\frac {1}{2}C_{2}{V_{2}}^{2} \\[ 5pt ] \frac {1}{2}\cdot \frac {2}{3}C{V_{1}}^{2}&=&\frac {1}{2}\cdot 3C{V_{2}}^{2} \\[ 5pt ] \frac {2}{3}{V_{1}}^{2}&=&3{V_{2}}^{2} \\[ 5pt ] {V_{1}}^{2}&=&\frac {9}{2}{V_{2}}^{2} \\[ 5pt ] V_{1}&=&\frac {3}{\sqrt {2}}V_{2}　　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。また，図1においてそれぞれのコンデンサに蓄えられる電荷が等しいことから，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
CV_{c}&=&2C\left( V_{1}-V_{c}\right) \\[ 5pt ] V_{c}&=&2\left( V_{1}-V_{c}\right) \\[ 5pt ] V_{c}&=&2V_{1}-2V_{c} \\[ 5pt ] 3V_{c}&=&2V_{1} \\[ 5pt ] V_{1}&=&\frac {3}{2}V_{c} \\[ 5pt ] \end{eqnarray}
\] となるので，これと①式より，
\[
\begin{eqnarray}
\frac {3}{2}V_{c}&=&\frac {3}{\sqrt {2}}V_{2} \\[ 5pt ] \frac {1}{\sqrt {2}}V_{c}&=&V_{2} \\[ 5pt ] \frac {V_{c}}{V_{2}}&=&\sqrt {2} \\[ 5pt ] \end{eqnarray}
\] と求められる。