Contents
【問題】
【難易度】★☆☆☆☆(易しい)
ある回路に\( i=4\sqrt {2} \sin 120 \pi t \ \mathrm {[A]} \ \)の電流が流れている。この電流の瞬時値が,時刻\( \ t = 0 \ \mathrm {[s]} \ \)以降に初めて\( \ 4 \ \mathrm {[A]} \ \)となるのは,時刻\( \ t = t_{1} \ \mathrm {[s]} \ \)である。\( \ t_{1} \ \mathrm {[s]} \ \)の値として,正しいのは次のうちどれか。
(1) \( \ \displaystyle \frac {1}{480} \ \) (2) \( \ \displaystyle \frac {1}{360} \ \) (3) \( \ \displaystyle \frac {1}{240} \ \) (4) \( \ \displaystyle \frac {1}{160} \ \) (5) \( \ \displaystyle \frac {1}{120} \ \)
【ワンポイント解説】
電流の瞬時値の式から,ある値に到達する時刻を求める問題です。
ほとんど物理というよりも数学の問題となりますが,電験では数学力は必須となりますので,必ず解けるようになって下さい。本問とは直接は関係ありませんが,瞬時値の概念と平均値及び実効値についてはしっかりと理解しておくようにしましょう。
1.正弦波交流の基本
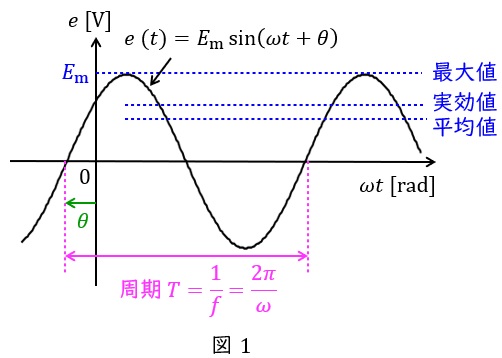
正弦波交流は図1に示されるような波形の交流です。
振幅の大きさ(最大値)を\( \ E_{\mathrm {m}} \ \mathrm {[V]} \ \),角速度を\( \ \omega \ \mathrm {[rad / s]} \ \),時間を\( \ t \ \mathrm {[s]} \ \),初期位相を\( \ \theta \ \mathrm {[rad]} \ \)とすれば,瞬時値\( \ e\left( t \right) \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( \omega t +\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,波形の周期\( \ T \ \mathrm {[s]} \ \)は,周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると,
\[
\begin{eqnarray}
T &=&\frac {1}{f}=\frac {2\pi }{\omega } \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,\( \ \omega =2\pi f \ \)となり,
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( 2\pi f t +\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と表現することもできます。
2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は,
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }E_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ]
&=&\frac {2}{\pi }E_{\mathrm {m}}
\end{eqnarray}
\]
となります。
②実効値\( \ F \ \)
定義式は,
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{E_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
時刻\( \ t = t_{1} \ \mathrm {[s]} \ \)のとき\( \ i=4 \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
4&=&4\sqrt {2} \sin 120 \pi t_{1} \\[ 5pt ]
\sin 120 \pi t_{1}&=&\frac {1}{\sqrt {2}} \\[ 5pt ]
120 \pi t_{1}&=&\frac {\pi }{4} \\[ 5pt ]
120 t_{1}&=&\frac {1}{4} \\[ 5pt ]
t_{1}&=&\frac {1}{480} \ \mathrm {[s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは