《理論》〈電気回路〉[H19:問7]RLC回路において抵抗で消費されるエネルギーに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

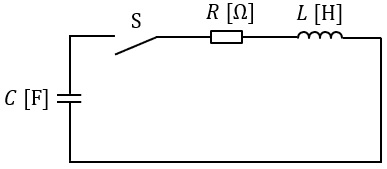
図に示す\( \ RLC \ \)回路において，静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサが電圧\( \ V \ \mathrm {[V]} \ \)に充電されている。この状態でスイツチ\( \ \mathrm {S} \ \)を閉じて，それから時間が十分に経過してコンデンサの端子電圧が最終的に零となった。この間に抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費された電気工ネルギ一\( \ \mathrm {[J]} \ \)を表す式として，正しいのは次のうちどれか。

　(1)　\( \ \displaystyle \frac {1}{2}C^{2}V \ \)　　(2)　\( \ \displaystyle \frac {1}{2}CV^{2} \ \)　　(3)　\( \ \displaystyle \frac {1}{2}\frac {V^{2}}{R} \ \)
　(4)　\( \ \displaystyle \frac {1}{2}L^{2}V \ \)　　(5)　\( \ \displaystyle \frac {1}{2}LV^{2} \ \)

【ワンポイント解説】

\( \ RLC \ \)回路において抵抗で消費されるエネルギーに関する問題です。
スイッチを閉じたあと回路内の電荷の動きがどのようになるかを考え，最終的には回路内には電流が流れなくなり，エネルギーがなくなることをイメージすればわかりやすいかと思います。

1.自己インダクタンス\( \ L \ \)と蓄積される電磁エネルギー\( \ W \ \)の関係式
自己インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルに電流\( \ I \ \mathrm {[A]} \ \)を流し，十分時間が経過した時にコイルに蓄えられるエネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W&=&\frac {1}{2}LI^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

2.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)が加わっているとすると，十分時間が経過した時にコンデンサに蓄えられる静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り，初期状態においてコンデンサに充電されるエネルギーは\( \ \displaystyle \frac {1}{2}CV^{2} \ \)であり，スイッチを閉じるとエネルギーが放出され，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費されると同時にリアクトル\( \ L \ \mathrm {[H]} \ \)にエネルギーが蓄えられる。
その後，リアクトル\( \ L \ \mathrm {[H]} \ \)に蓄えられたエネルギーにより，コンデンサ\( \ C \ \mathrm {[F]} \ \)に逆極性に充電される。
さらに時間が経過すると，コンデンサ\( \ C \ \mathrm {[F]} \ \)に逆極性に蓄えられた電荷が放出され，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費されると同時にリアクトル\( \ L \ \mathrm {[H]} \ \)にエネルギーが蓄えられ，以降これを繰り返す。
以上から，最終的にはコンデンサ\( \ C \ \mathrm {[F]} \ \)の電荷が全て放出されエネルギーが零，回路内の電流が零となるためリアクトル\( \ L \ \mathrm {[H]} \ \)のエネルギーも零，すなわちコンデンサ\( \ C \ \mathrm {[F]} \ \)に充電されたエネルギーは全て抵抗\( \ R \ \mathrm {[\Omega ]} \ \)でで消費されることになる。
したがって，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)で消費されたエネルギーは\( \ \displaystyle \frac {1}{2}CV^{2} \ \)と求められる。