Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
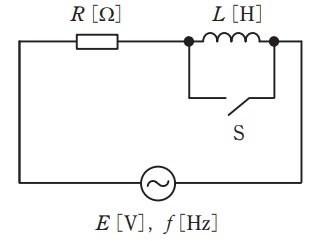
図のように,周波数\( \ f \ \mathrm {[Hz]} \ \)の交流電圧\( \ E \ \mathrm {[V]} \ \)の電源に,\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗,インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルとスイッチ\( \ \mathrm {S} \ \)を接続した回路がある。スイッチ\( \ \mathrm {S} \ \)が開いているときに回路が消費する電力\( \ \mathrm {[W]} \ \)は,スイッチ\( \ \mathrm {S} \ \)が閉じているときに回路が消費する電力\( \ \mathrm {[W]} \ \)の\( \ \displaystyle \frac {1}{2} \ \)になった。このとき,\( \ L \ \mathrm {[H]} \ \)の値を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 2\pi fR \ \) (2) \( \ \displaystyle \frac {R}{2\pi f} \ \) (3) \( \ \displaystyle \frac {2\pi f}{R} \ \) (4) \( \ \displaystyle \frac {\left( 2\pi f\right) ^{2}}{R} \ \) (5) \( \ \left( 2\pi f \right) ^{2}R \ \)
【ワンポイント解説】
交流回路の各インピーダンスの特性を理解しているかを問う問題です。
最初はイメージを掴むため,リアクトル導通前後のベクトル図を描いても良いかと思います。
また,「消費する電力\( \ \mathrm {[W]} \ \)」というのは,抵抗で消費する有効電力のことを指していることを問題文から読み解けるようにしましょう。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
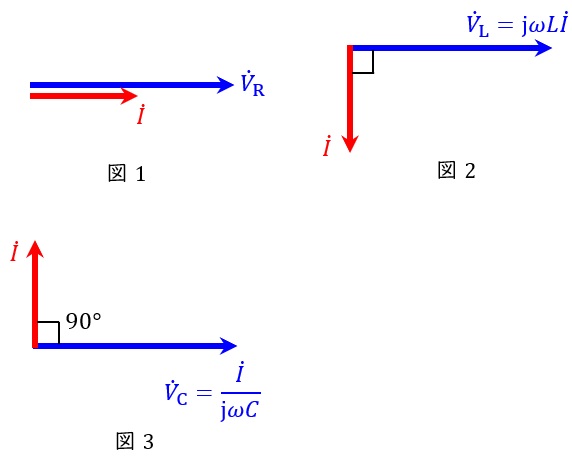
となります。この関係をベクトル図に表すと,図1~図3となります。
2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
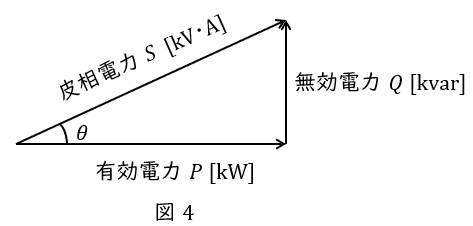
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \),リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び,図4のようにベクトル図を描きます。さらに,有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ,
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。図4において,力率は\( \ \cos \theta \ \)で定義され,
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ]
\end{eqnarray}
\]
となります。
また,線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \),有効電力\( \ P \ \mathrm {[W]} \ \),無効電力\( \ Q \ \mathrm {[var]} \ \)は,インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \),抵抗を\( \ R \ \mathrm {[\Omega ]} \ \),リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ]
P &=&RI^{2} \\[ 5pt ]
Q &=&XI^{2} \\[ 5pt ]
\end{eqnarray}
\]
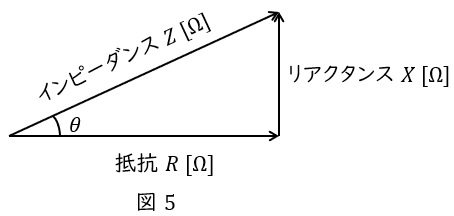
となるため,\( \ Z \ \mathrm {[\Omega ]} \ \),\( \ R \ \mathrm {[\Omega ]} \ \),\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図5のような関係を描くことができます。
【解答】
解答:(2)
ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」より,スイッチ開放前後の回路の電流を\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
{\dot I}_{1} &=&\frac {\dot E}{R} \\[ 5pt ]
{\dot I}_{2} &=&\frac {\dot E}{R+\mathrm {j}2\pi fL} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ I_{1} \ \mathrm {[A]} \ \)及び\( \ I_{2} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1} &=&\frac {E}{R} \\[ 5pt ]
I_{2} &=&\frac {E}{\sqrt {R^{2}+\left( 2\pi f L\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り,消費電力\( \ P \ \mathrm {[W]} \ \)は電流\( \ I \ \mathrm {[A]} \ \)の\( \ 2 \ \)乗に比例するので,インダクタンスを接続することで消費電力が\( \ \displaystyle \frac {1}{2} \ \)になったということは電流は\( \ \displaystyle \frac {1}{\sqrt {2}} \ \)になったということになる。したがって,
\[
\begin{eqnarray}
I_{1} &=&\sqrt {2}I_{2} \\[ 5pt ]
\frac {E}{R} &=&\sqrt {2}\cdot \frac {E}{\sqrt {R^{2}+\left( 2\pi f L\right) ^{2}}} \\[ 5pt ]
\frac {1}{R} &=&\frac {\sqrt {2}}{\sqrt {R^{2}+\left( 2\pi f L\right) ^{2}}} \\[ 5pt ]
\frac {1}{R^{2}} &=&\frac {2}{R^{2}+\left( 2\pi f L\right) ^{2}} \\[ 5pt ]
R^{2}+\left( 2\pi f L\right) ^{2} &=&2R^{2} \\[ 5pt ]
\left( 2\pi f L\right) ^{2} &=&R^{2} \\[ 5pt ]
2\pi f L &=&R \\[ 5pt ]
L &=&\frac {R}{2\pi f} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは