Contents
【問題】
【難易度】★★★★☆(やや難しい)
図1は,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサとコイルからなる共振回路の等価回路である。このようにコイルに内部抵抗\( \ r \ \mathrm {[\Omega ]} \ \)が存在する場合は,インダクタンス\( \ L \ \mathrm {[H]} \ \)と抵抗\( \ r \ \mathrm {[\Omega ]} \ \)の直列回路として表すことができる。 この直列回路は,コイルの抵抗\( \ r \ \mathrm {[\Omega ]} \ \)が,誘導性リアクタンス\( \ \omega L \ \mathrm {[\Omega ]} \ \)に比べて十分小さいものとすると,図2のように,等価抵抗\( \ R_{\mathrm {p}} \ \mathrm {[\Omega ]} \ \)とインダクタンス\( \ L \ \mathrm {[H]} \ \)の並列回路に変換することができる。このときの等価抵抗\( \ R_{\mathrm {p}} \ \mathrm {[\Omega ]} \ \)の値を表す式として,正しいのは次のうちどれか。
ただし,\( \ I_{\mathrm {c}} \ \mathrm {[A]} \ \)は電流源の電流を表す。
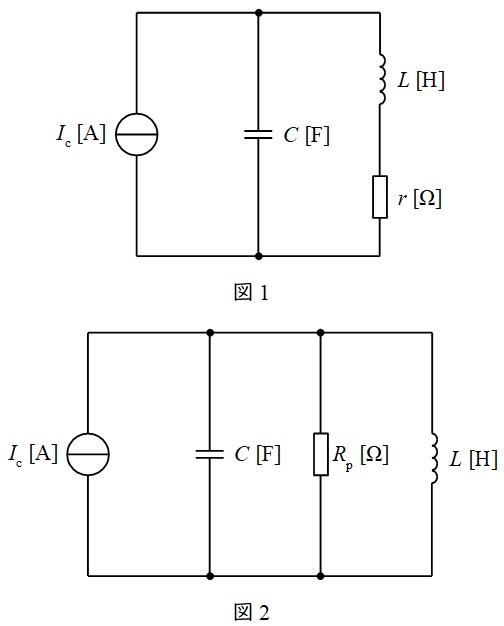
(1) \( \ \displaystyle \frac {\omega L}{r} \ \) (2) \( \ \displaystyle \frac {r}{\left( \omega L\right) ^{2}} \ \) (3) \( \ \displaystyle \frac {r^{2}}{\omega L} \ \) (4) \( \ \displaystyle \frac {\left( \omega L\right) ^{2}}{r} \ \) (5) \( \ r\left( \omega L\right) ^{2} \ \)
【ワンポイント解説】
等価抵抗を求める問題です。問題文に共振回路と書いてありますが,本問においては共振回路の考え方は適用せず,普通にアドミタンスを求めて解く必要があります。
例外はありますが,一般に近似計算においては\( \ \Delta x \ \)が\( \ x \ \)より十分に小さいとき,
\[
\begin{eqnarray}
\left( x+\Delta x \right) ^{2}&=&x^{2}+2x\cdot \Delta x+\left( \Delta x\right) ^{2} \\[ 5pt ]
&≃&x^{2}+2x\cdot \Delta x \\[ 5pt ]
\end{eqnarray}
\]
と\( \ 2 \ \)乗以降の項を無視して計算します。
1.抵抗,コイル,コンデンサのインピーダンスとアドミタンス
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンス\( \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,アドミタンス\( \ \mathrm {[S]} \ \)はインピーダンスの逆数なので,
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {R}}&=&\frac {1}{R}&& \\[ 5pt ]
{\dot Y}_{\mathrm {L}}&=&\frac {1}{\mathrm {j}\omega L}&=&\frac {1}{\mathrm {j}2\pi f L} \\[ 5pt ]
{\dot Y}_{\mathrm {C}}&=&\mathrm {j}\omega C&=&\mathrm {j}2\pi f C \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.合成インピーダンス
インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ \)と\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時,直列及び並列の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。
①直列
直列合成インピーダンス\( \ {\dot Z} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}&=&{\dot Z}_{1}+{\dot Z}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成インピーダンス\( \ {\dot Z} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{{\dot Z}}&=&\frac {1}{{\dot Z}_{1}}+\frac {1}{{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
{\dot Z}&=&\frac {{\dot Z}_{1}{\dot Z}_{2}}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.合成アドミタンス
アドミタンス\( \ {\dot Y}_{1} \ \mathrm {[S]} \ \)と\( \ {\dot Y}_{2} \ \mathrm {[S]} \ \)が与えられている時,直列及び並列の合成アドミタンス\( \ \dot Y \ \mathrm {[S]} \ \)は以下の式で与えられます。
①直列
直列合成アドミタンス\( \ {\dot Y} \ \mathrm {[S]} \ \)は,
\[
\begin{eqnarray}
\frac {1}{{\dot Y}}&=&\frac {1}{{\dot Y}_{1}}+\frac {1}{{\dot Y}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,整理すると,
\[
\begin{eqnarray}
{\dot Y}&=&\frac {{\dot Y}_{1}{\dot Y}_{2}}{{\dot Y}_{1}+{\dot Y}_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
並列合成アドミタンス\( \ {\dot Y} \ \mathrm {[S]} \ \)は,
\[
\begin{eqnarray}
{\dot Y}&=&{\dot Y}_{1}+{\dot Y}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(4)
\( \ r \ \mathrm {[\Omega ]} \ \)と\( \ \omega L \ \mathrm {[\Omega ]} \ \)の合成インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサのインピーダンスとアドミタンス」及び「2.合成インピーダンス」の通り,
\[
\begin{eqnarray}
{\dot Z}_{1}&=&r+\mathrm {j}\omega L \\[ 5pt ]
\end{eqnarray}
\]
であるので,図1の合成アドミタンス\( \ {\dot Y}_{1} \ \mathrm {[S]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサのインピーダンスとアドミタンス」及び「3.合成アドミタンス」の通り,
\[
\begin{eqnarray}
{\dot Y}_{1}&=&\mathrm {j}\omega C+\frac {1}{{\dot Z}_{1}} \\[ 5pt ]
&=&\mathrm {j}\omega C+\frac {1}{r+\mathrm {j}\omega L} \\[ 5pt ]
&=&\mathrm {j}\omega C+\frac {1}{r+\mathrm {j}\omega L}\times \frac {r-\mathrm {j}\omega L}{r-\mathrm {j}\omega L} \\[ 5pt ]
&=&\mathrm {j}\omega C+\frac {r-\mathrm {j}\omega L}{r^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ]
&=&\frac {r}{r^{2}+\left( \omega L\right) ^{2}}+\mathrm {j}\left\{ \omega C-\frac {\omega L}{r^{2}+\left( \omega L\right) ^{2}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \omega L ≫r \ \)であるから,
\[
\begin{eqnarray}
{\dot Y}_{1}&≃&\frac {r}{\left( \omega L\right) ^{2}}+\mathrm {j}\left\{ \omega C-\frac {\omega L}{\left( \omega L\right) ^{2}}\right\} \\[ 5pt ]
&=&\frac {r}{\left( \omega L\right) ^{2}}+\mathrm {j}\left( \omega C-\frac {1}{\omega L}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,図2の合成アドミタンス\( \ {\dot Y}_{2} \ \mathrm {[S]} \ \)は,ワンポイント解説「1.抵抗,コイル,コンデンサのインピーダンスとアドミタンス」及び「3.合成アドミタンス」の通り,
\[
\begin{eqnarray}
{\dot Y}_{2}&=&\mathrm {j}\omega C+\frac {1}{R_{\mathrm {p}}}+\frac {1}{\mathrm {j}\omega L} \\[ 5pt ]
&=&\frac {1}{R_{\mathrm {p}}}+\mathrm {j}\left( \omega C-\frac {1}{\omega L}\right) \left( ∵\frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ {\dot Y}_{1} \ \mathrm {[S]} \ \)と\( \ {\dot Y}_{2} \ \mathrm {[S]} \ \)は等しくなければならないから,係数比較すると,
\[
\begin{eqnarray}
\frac {r}{\left( \omega L\right) ^{2}}&=&\frac {1}{R_{\mathrm {p}}} \\[ 5pt ]
R_{\mathrm {p}}&=&\frac {\left( \omega L\right) ^{2}}{r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
図1及び図2共に電流源とコンデンサ\( \ C \ \)の接続は同じなので,図1の\( \ r \ \mathrm {[\Omega ]} \ \)と\( \ \omega L \ \mathrm {[\Omega ]} \ \)の合成アドミタンスと図2の\( \ R_{\mathrm {p}} \ \mathrm {[\Omega ]} \ \)と\( \ \omega L \ \mathrm {[\Omega ]} \ \)の合成アドミタンスが等しくなればよい。したがって,
\[
\begin{eqnarray}
\frac {1}{r+\mathrm {j}\omega L}&=&\frac {1}{R_{\mathrm {p}}}+\frac {1}{\mathrm {j}\omega L} \\[ 5pt ]
\frac {1}{R_{\mathrm {p}}}+\frac {1}{\mathrm {j}\omega L}&=&\frac {1}{r+\mathrm {j}\omega L}\times \frac {r-\mathrm {j}\omega L}{r-\mathrm {j}\omega L} \\[ 5pt ]
\frac {1}{R_{\mathrm {p}}}-\mathrm {j}\frac {1}{\omega L}&=&\frac {r-\mathrm {j}\omega L}{r^{2}+\left( \omega L\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \omega L ≫r \ \)であるから,
\[
\begin{eqnarray}
\frac {1}{R_{\mathrm {p}}}-\mathrm {j}\frac {1}{\omega L}&≃&\frac {r-\mathrm {j}\omega L}{\left( \omega L\right) ^{2}} \\[ 5pt ]
&=&\frac {r}{\left( \omega L\right) ^{2}}-\mathrm {j}\frac {1}{\omega L} \\[ 5pt ]
\end{eqnarray}
\]
となる。実部を比較すれば,
\[
\begin{eqnarray}
\frac {1}{R_{\mathrm {p}}}&=&\frac {r}{\left( \omega L\right) ^{2}} \\[ 5pt ]
R_{\mathrm {p}}&=&\frac {\left( \omega L\right) ^{2}}{r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは