Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,直流電流計の測定範囲拡大について述べたものである。
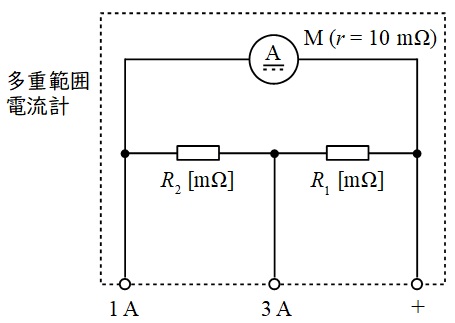
内部抵抗\( \ r=10 \ \mathrm {[m\Omega ]} \ \),最大目盛\( \ 0.5 \ \mathrm {[A]} \ \)の直流電流計\( \ \mathrm {M} \ \)がある。この電流計と抵抗\( \ R_{1} \ \mathrm {[m\Omega ]} \ \)及び\( \ R_{2} \ \mathrm {[m\Omega ]} \ \)を図のように結線し,最大目盛が\( \ 1 \ \mathrm {[A]} \ \)と\( \ 3 \ \mathrm {[A]} \ \)からなる多重範囲電流計を作った。この多重範囲電流計において,端子\( \ 3 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合,抵抗\( \ \fbox { (ア) } \ \mathrm {[m\Omega ]} \ \)が分流器となる。端子\( \ 1 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合には,抵抗\( \ \fbox { (イ) } \ \mathrm {[m\Omega ]} \ \)が倍率\( \ \fbox { (ウ) } \ \)倍の分流器となる。また,\( \ 3 \ \mathrm {[A]} \ \)を最大目盛とする多重範囲電流計の内部抵抗は\( \ \fbox { (エ) } \ \mathrm {[m\Omega ]} \ \)となる。
上記の記述中の空白箇所 (ア),(イ),(ウ)及び(エ)に当てはまる式又は数値として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & R_{2} & R_{1} & \displaystyle \frac {10+R_{2}}{R_{1}}+1 & \displaystyle \frac {20}{3} \\
\hline
(2) & R_{1} & R_{1}+R_{2} & \displaystyle \frac {10+R_{2}}{R_{1}} & \displaystyle \frac {25}{9} \\
\hline
(3) & R_{2} & R_{1}+R_{2} & \displaystyle \frac {10}{R_{1}+R_{2}}+1 & 5 \\
\hline
(4) & R_{1} & R_{2} & \displaystyle \frac {10}{R_{1}+R_{2}} & \displaystyle \frac {10}{3} \\
\hline
(5) & R_{1} & R_{1}+R_{2} & \displaystyle \frac {10}{R_{1}+R_{2}}+1 & \displaystyle \frac {25}{9} \\
\hline
\end{array}
\]
【ワンポイント解説】
分流器による直流電流計の測定範囲拡大とその倍率の導出に関する問題です。
各端子を接続したときにどの抵抗が分流器になるか考えて解いていきましょう。
(エ)の選択肢はやや難易度は高いですが,わからなくても(ア)~(ウ)の空欄で正答が導き出せるので,正答すること自体は難しくない問題といえると思います。
1.分流器
電流計に並列につなぐ抵抗器のことで,電流計の測定できる範囲を拡大することができるものです。図1のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \),分流器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると,電流計に流れる電流\( \ I_{\mathrm {m}} \ \mathrm {[A]} \ \)は,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {m}} &=&\frac {R}{R+r}I \\[ 5pt ]
\end{eqnarray}
\]
となり,倍率\( \ \displaystyle m=\frac {I}{I_{\mathrm {m}}} \ \)は,
\[
\begin{eqnarray}
m&=&\frac {I}{I_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {R+r}{R} \\[ 5pt ]
&=&1+\frac {r}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって,分流器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは,
\[
\begin{eqnarray}
m&=&1+\frac {r}{R} \\[ 5pt ]
\frac {r}{R}&=&m-1 \\[ 5pt ]
R&=&\frac {r}{m-1} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。

2.倍率器
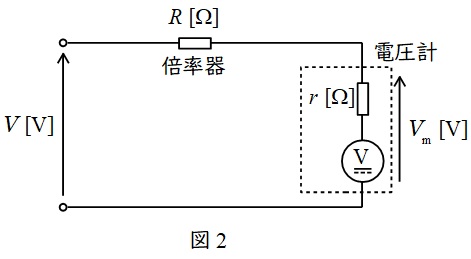
電圧計に直列につなぐ抵抗器のことで,電圧計の測定できる範囲を拡大することができるものです。図2のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \),倍率器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると,電圧計にかかる電圧\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&\frac {r}{R+r}V \\[ 5pt ]
\end{eqnarray}
\]
となり,倍率\( \ \displaystyle m=\frac {V}{V_{\mathrm {m}}} \ \)は,
\[
\begin{eqnarray}
m&=&\frac {V}{V_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {R+r}{r} \\[ 5pt ]
&=&1+\frac {R}{r} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって,倍率器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは,
\[
\begin{eqnarray}
m&=&1+\frac {R}{r} \\[ 5pt ]
\frac {R}{r}&=&m-1 \\[ 5pt ]
R&=&\left( m-1\right) r\\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
解答:(5)
(ア)
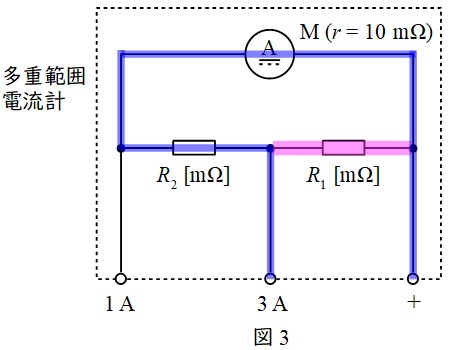
ワンポイント解説「1.分流器」及び図3に示す通り,端子\( \ 3 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合,分流器は\( \ R_{1} \ \)となります。
(イ)
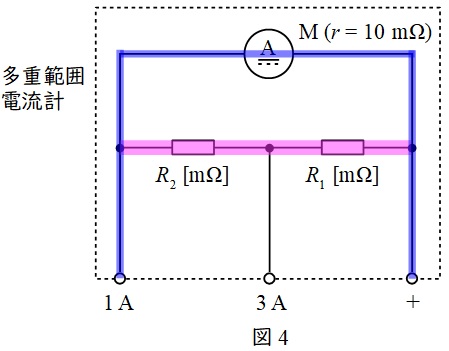
ワンポイント解説「1.分流器」及び図4に示す通り,端子\( \ 1 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合,分流器は\( \ R_{1}+R_{2} \ \)となります。
(ウ)
端子\( \ 1 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合の分流器の倍率\( \ \displaystyle m_{1} \ \)は,ワンポイント解説「1.分流器」の通り,
\[
\begin{eqnarray}
m_{1}&=&\frac {M}{R_{1}+R_{2}}+1 \\[ 5pt ]
&=&\frac {10}{R_{1}+R_{2}}+1 \\[ 5pt ]
\end{eqnarray}
\]
となります。
(エ)
端子\( \ 3 \ \mathrm {A} \ \)と端子\( \ + \ \)を使用する場合の分流器の倍率\( \ \displaystyle m_{3} \ \)は,ワンポイント解説「1.分流器」の通り,
\[
\begin{eqnarray}
m_{3}&=&\frac {M+R_{2}}{R_{1}}+1 \\[ 5pt ]
&=&\frac {10+R_{2}}{R_{1}}+1 \\[ 5pt ]
\end{eqnarray}
\]
となる。図3において,直流電流計に\( \ I_{\mathrm {m}}=0.5 \ \mathrm {[A]} \ \)を流したときに各端子に流れる電流\( \ I=3.0 \ \mathrm {[A]} \ \)であるから,\( \ m_{3}=6 \ \)を上式に代入すると,
\[
\begin{eqnarray}
6&=&\frac {10+R_{2}}{R_{1}}+1 \\[ 5pt ]
\frac {10+R_{2}}{R_{1}}&=&5 \\[ 5pt ]
10+R_{2}&=&5R_{1} \\[ 5pt ]
5R_{1}-R_{2}&=&10 ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に,図4において,直流電流計に\( \ I_{\mathrm {m}}=0.5 \ \mathrm {[A]} \ \)を流したときに各端子に流れる電流\( \ I=1.0 \ \mathrm {[A]} \ \)であるから,\( \ m_{1}=2 \ \)を(ウ)解答式に代入すると,
\[
\begin{eqnarray}
m_{1}&=&\frac {10}{R_{1}+R_{2}}+1 \\[ 5pt ]
2&=&\frac {10}{R_{1}+R_{2}}+1 \\[ 5pt ]
\frac {10}{R_{1}+R_{2}}&=&1 \\[ 5pt ]
R_{1}+R_{2}&=&10 ・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。①+②より,
\[
\begin{eqnarray}
6R_{1}&=&20 \\[ 5pt ]
R_{1}&=&\frac {10}{3} \ \mathrm {[m\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを②に代入すると,
\[
\begin{eqnarray}
R_{1}+R_{2}&=&10 \\[ 5pt ]
\frac {10}{3}+R_{2}&=&10 \\[ 5pt ]
R_{2}&=&10-\frac {10}{3} \\[ 5pt ]
&=&\frac {20}{3} \ \mathrm {[m\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,図3における合成インピーダンス\( \ R \ \mathrm {[m\Omega ]} \ \)は,
\[
\begin{eqnarray}
R&=&\frac {R_{1}\left( M+R_{2}\right) }{R_{1}+\left( M+R_{2}\right) } \\[ 5pt ]
&=&\frac {\displaystyle \frac {10}{3}\times \left( 10+\frac {20}{3}\right) }{\displaystyle \frac {10}{3}+\left( 10+\frac {20}{3}\right) } \\[ 5pt ]
&=&\frac {\displaystyle \frac {500}{9}}{20} \\[ 5pt ]
&=&\frac {25}{9} \ \mathrm {[m\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは