《理論》〈電気回路〉[H22:問7]単相3線式回路に平衡負荷を接続したときの消費電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

抵抗\( \ R = 4 \ \mathrm {[\Omega ]} \ \)と誘導性リアクタンス\( \ X = 3 \ \mathrm {[\Omega ]} \ \)が直列に接続された負荷を，図のように線間電圧\( \ {\dot V}_{\mathrm {ab}}=100∠0° \ \mathrm {[V]} \ \)，\( \ {\dot V}_{\mathrm {bc}}=100∠0° \ \mathrm {[V]} \ \)の単相\( \ 3 \ \)線式電源に接続した。このとき，これらの負荷で消費される総電力\( \ P \ \mathrm {[W]} \ \)の値として，正しいのは次のうちどれか。

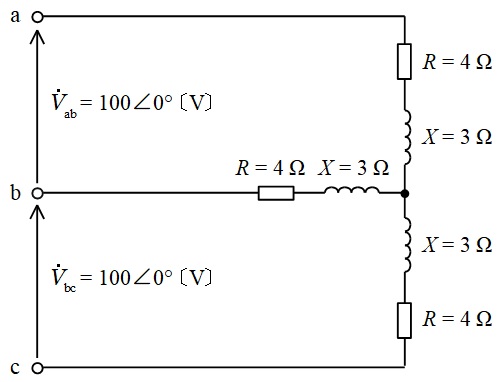
　(1)　\( \ 800 \ \)　　(2)　\( \ 1 \ 200 \ \)　　(3)　\( \ 3 \ 200 \ \)　　(4)　\( \ 3 \ 600 \ \)　　(5)　\( \ 4 \ 800 \ \)

【ワンポイント解説】

単相\( \ 3 \ \)線式線路における消費電力を求める問題です。
内容としてはどちらかと言えば電力科目に分類される問題ですが，総合的な能力を問われている問題と言えるかと思います。
単相\( \ 3 \ \)線式線路の特徴はしっかりと覚えておきましょう。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
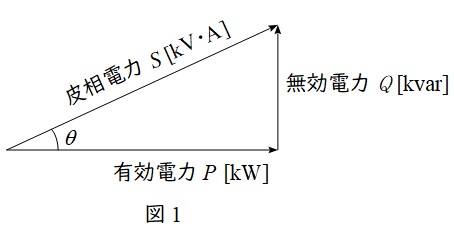
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

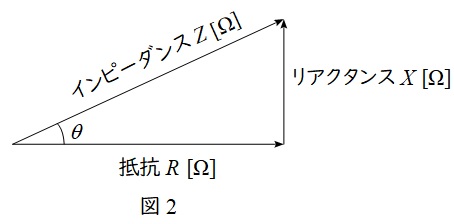
また，線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき，皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)，有効電力\( \ P \ \mathrm {[W]} \ \)，無効電力\( \ Q \ \mathrm {[var]} \ \)は，インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \)，抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)，リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ] P &=&RI^{2} \\[ 5pt ] Q &=&XI^{2} \\[ 5pt ] \end{eqnarray}
\] となるため，\( \ Z \ \mathrm {[\Omega ]} \ \)，\( \ R \ \mathrm {[\Omega ]} \ \)，\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図2のような関係を描くことができます。

2.単相\( \ 3 \ \)線式配電方式
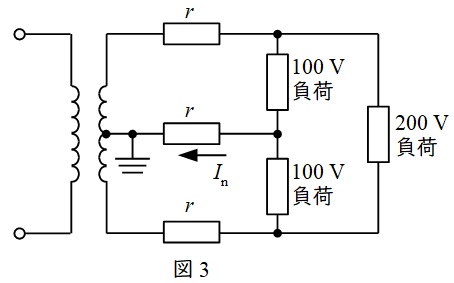
単相\( \ 3 \ \)線式配電方式は図3のような回路で低圧の需要家に配電する方式で以下のような特徴があります。
・\( \ 100 \ \mathrm {[V]} \ \)負荷と\( \ 200 \ \mathrm {[V]} \ \)負荷の双方に供給可能
・線路負荷が平衡している時，中性点電流\( \ I_{\mathrm {n}} \ \)は零となる
・線路負荷が平衡しており，線間電圧，線電流が等しい場合，単相\( \ 2 \ \)線式に比べ線路電流は\( \ \displaystyle \frac {1}{2} \ \)となるので，線路損失は\( \ \displaystyle \frac {1}{4} \ \)となる

【解答】

解答：(3)
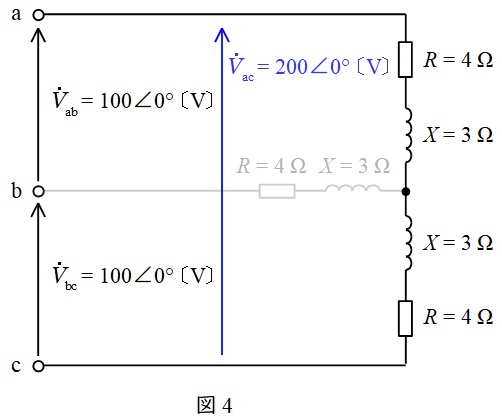
問題図において負荷は平衡しているので，ワンポイント解説「2.単相\( \ 3 \ \)線式配電方式」の通り，中性線\( \ \mathrm {b} \ \)には電流が流れない。したがって，回路図は図4のように書き換えられる。
図4において，負荷のインピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)の大きさは，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
Z &=&\sqrt {\left( R+R\right) ^{2}+\left( X+X\right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( 4+4\right) ^{2}+\left( 3+3\right) ^{2}} \\[ 5pt ] &=&10 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，負荷を流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I &=&\frac {V_{\mathrm {ac}}}{Z} \\[ 5pt ] &=&\frac {200}{10} \\[ 5pt ] &=&20 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷で消費される電力\( \ P \ \mathrm {[W]} \ \)は，ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，
\[
\begin{eqnarray}
P &=&RI^{2}+RI^{2} \\[ 5pt ] &=&2RI^{2} \\[ 5pt ] &=&2\times 4\times 20^{2} \\[ 5pt ] &=&3 \ 200 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。