《理論》〈電磁気〉[R01:問2]平行平板コンデンサの電界に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，極板間距離$\ d \ \mathrm {[mm]} \ $と比誘電率$\ \varepsilon _{\mathrm {r}} \ $が異なる平行板コンデンサが接続されている。極板の形状と大きさは全て同一であり，コンデンサの端効果，初期電荷及び漏れ電流は無視できるものとする。印加電圧は$\ 10 \ \mathrm {kV} \ $とするとき，図中の二つのコンデンサ内部の電界の強さ$\ E_{\mathrm {A}} \ $及び$\ E_{\mathrm {B}} \ $の値$\ \mathrm {[kV／mm]} \ $の組み合わせとして，正しいものを次の(1)～(5)のうちから一つ選べ。

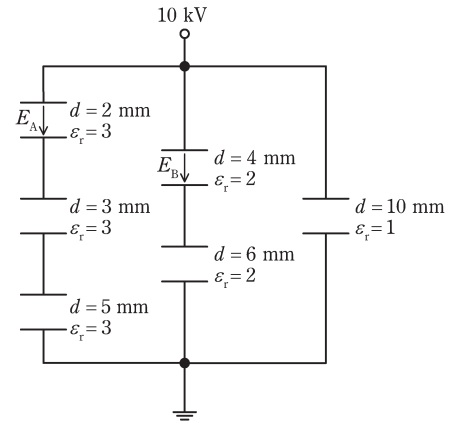
$$\begin{array}{cccc} & E_{\mathrm {A}} & E_{\mathrm {B}} \\ \hline (1) & 　0.25　 & 　0.67　 \\ \hline (2) & 　0.25　 & 　1.5　 \\ \hline (3) & 　1.0　 & 　1.0　 \\ \hline (4) & 　4.0　 & 　0.67　 \\ \hline (5) & 　4.0　 & 　1.5　 \\ \hline \end{array}$$

【ワンポイント解説】

毎年のように出題される平行平板コンデンサに関する問題ですが，毎年出題されているので少しひねったような出題をされています。どのような問題が出題されても基本的に使用する公式は同じ公式です。

1.平行平板コンデンサの極板間に蓄えられる電荷$\ Q \ $
静電容量$\ C \ $の平行平板コンデンサに電圧$\ V \ $をかけて十分時間が経った時，コンデンサに蓄えられる電荷$\ Q \ $は，

$$\begin{eqnarray} Q &=&CV \\[ 5pt ] \end{eqnarray}$$ となります。

2.平行平板コンデンサの静電容量$\ C \ $
平行平板コンデンサの静電容量$\ C \ $は，真空の誘電率を$\ \varepsilon _{0} \ $，極板の面積を$\ S \ $，極板間の距離を$\ d \ $とすると，

$$\begin{eqnarray} C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}$$ となります。平行平板コンデンサの間に比誘電率$\ \varepsilon _{\mathrm {r}} \ $の誘電体を挿入すると，
$$\begin{eqnarray} C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}$$ となります。

3.平行平板コンデンサの極板間の電界$\ E \ $
極板間の距離$\ d \ $の平行平板コンデンサに，電圧$\ V \ $の電源を接続すると，極板間の電界$\ E \ $は，

$$\begin{eqnarray} E &=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

解答：(3)
問題図のコンデンサにおいては直列に繋がれているコンデンサの比誘電率はすべて等しいので，問題図は図1のように書き換えることができる。

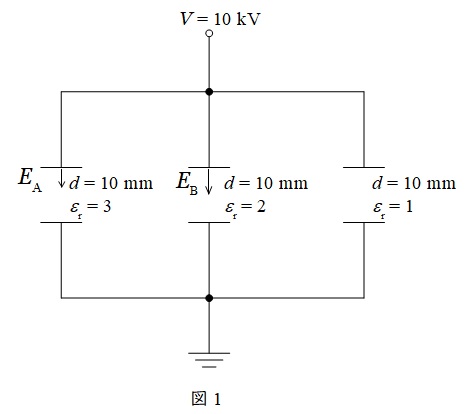
図1より平行平板コンデンサ内の電界は一様であるから，ワンポイント解説「3.平行平板コンデンサの極板間の電界$\ E \ $」より，

$$\begin{eqnarray} E_{\mathrm {A}} &=&\frac {V}{d} \\[ 5pt ] &=&\frac {10}{10} \\[ 5pt ] &=&1.0 \ \mathrm {[kV／mm]} \\[ 5pt ] \end{eqnarray}$$ $$\begin{eqnarray} E_{\mathrm {B}} &=&\frac {V}{d} \\[ 5pt ] &=&\frac {10}{10} \\[ 5pt ] &=&1.0 \ \mathrm {[kV／mm]} \\[ 5pt ] \end{eqnarray}$$ と求められる。