《理論》〈電気回路〉[H23:問9]抵抗とコンデンサを直列接続した交流回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，$\ 1 \ 000 \ \mathrm {[\Omega ]} \ $の抵抗と静電容量$\ C \ \mathrm {[\mu F ]} \ $のコンデンサを直列に接続した交流回路がある。いま，電源の周波数が$\ 1 \ 000 \ \mathrm {[Hz]} \ $のとき，電源電圧$\ \dot E \ \mathrm {[V]} \ $と電流$\ \dot I \ \mathrm {[A]} \ $の位相差は$\ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ $であった。このとき，コンデンサの静電容量$\ C \ \mathrm {[\mu F ]} \ $の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 0.053 \ $　　(2)　$\ 0.092 \ $　　(3)　$\ 0.107 \ $　　(4)　$\ 0.159 \ $　　(5)　$\ 0.258 \ $

【ワンポイント解説】

交流回路における$\ RC \ $直列回路の計算に関する問題です。
直列回路においては，回路に流れる電流を基準にベクトル図を記載することを覚えておきましょう。

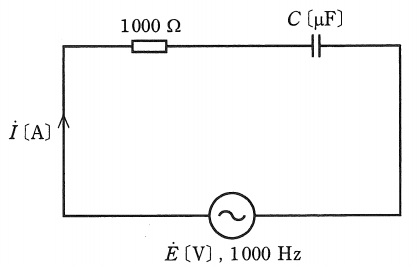
1.抵抗，コイル，コンデンサの電圧$\ V \ \mathrm {[V]} \ $と電流$\ I \ \mathrm {[A]} \ $の関係
抵抗$\ R \ \mathrm {[\Omega ]} \ $，コイル$\ L \ \mathrm {[H]} \ $，コンデンサ$\ C \ \mathrm {[F]} \ $があり，電源周波数$\ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
$$\begin{eqnarray} {\dot Z}_{\mathrm {R}}&=&R && \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}$$ で求められ，それぞれの電圧と電流の関係は，
$$\begin{eqnarray} {\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I&=&\mathrm {j}2\pi f L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C}&=&\frac {\dot I }{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}$$ となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(2)
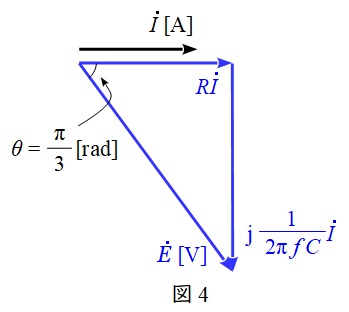
ワンポイント解説「1.抵抗，コイル，コンデンサの電圧$\ V \ \mathrm {[V]} \ $と電流$\ I \ \mathrm {[A]} \ $の関係」に沿って，ベクトル図を描くと図4のようになる。
$\ \dot E \ \mathrm {[V]} \ $と$\ \dot I \ \mathrm {[A]} \ $の位相差$\ \theta \ $は$\ \displaystyle \theta =\frac {\pi }{3} \ \mathrm {[rad]} \ $であるから，
$$\begin{eqnarray} \tan \theta &=&\frac {\displaystyle \frac {I}{2\pi f C}}{RI} \\[ 5pt ] &=&\frac {1}{2\pi f CR} \\[ 5pt ] C&=&\frac {1}{2\pi f R\tan \theta } \\[ 5pt ] &=&\frac {1}{2\pi \times 1000 \times 1000\times \sqrt {3} } \\[ 5pt ] &≒&9.19\times 10^{-8} \ \mathrm {[F]}　→　0.092 \ \mathrm {[\mu F ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。