Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図1は,二重積分形\( \ \mathrm {A-D} \ \)変換器を用いたディジタル直流電圧計の原理図である。次の(a)及び(b)の問に答えよ。
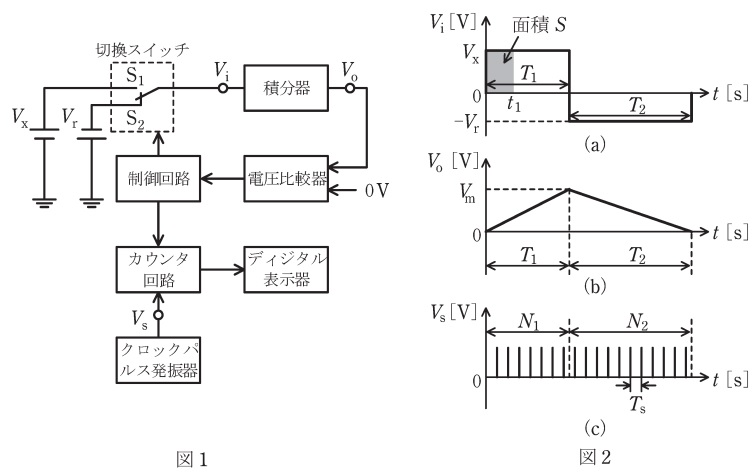
(a) 図1のように,負の基準電圧\( \ -V_{\mathrm {r}}(V_{\mathrm {r}}>0) \ \mathrm {[V]} \ \)と切換スイッチが接続された回路があり,その回路を用いて正の未知電圧\( \ V_{\mathrm {x}}(>0) \ \mathrm {[V]} \ \)を測定する。まず,制御回路によってスイッチが\( \ \mathrm {S}_{1} \ \)側へ切り換わると,時刻\( \ t=0 \ \mathrm {s} \ \)で測定電圧\( \ V_{\mathrm {x}} \ \mathrm {[V]} \ \)が積分器へ入力される。その入力電圧\( \ V_{\mathrm {i}} \ \mathrm {[V]} \ \)の時間変化が図2(a)であり,積分器からの出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)の時間変化が図2(b)である。ただし,\( \ t=0 \ \mathrm {s} \ \)での出力電圧を\( \ V_{\mathrm {o}}=0 \ \mathrm {V} \ \)とする。時刻\( \ t_{1} \ \)における\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は,入力電圧\( \ V_{\mathrm {i}} \ \mathrm {[V]} \ \)の期間\( \ 0~t_{1} \ \mathrm {[s]} \ \)で囲われる面積\( \ S \ \)に比例する。積分器の特性で決まる比例定数を\( \ k(>0) \ \)とすると,時刻\( \ t=T_{1} \ \mathrm {[s]} \ \)のときの出力電圧は,\( \ V_{\mathrm {m}}= \ \fbox { (ア) } \ \ \mathrm {[V]} \ \)となる。
定められた時刻\( \ t=T_{1} \ \mathrm {[s]} \ \)に達すると,制御回路によってスイッチが\( \ \mathrm {S}_{2} \ \)側に切り換わり,積分器には基準電圧\( \ -V_{\mathrm {r}} \ \mathrm {[V]} \ \)が入力される。よって,スイッチ\( \ \mathrm {S}_{2} \ \)の期間中の時刻\( \ t \ \mathrm {[s]} \ \)における積分器の出力電圧の大きさは,\( \ V_{\mathrm {o}}=V_{\mathrm {m}}- \ \fbox { (イ) } \ \mathrm {[V]} \ \)と表される。
積分器の出力電圧\( \ V_{\mathrm {o}} \ \)が\( \ 0 \ \mathrm {V} \ \)になると,電圧比較器がそれを検出する。\( \ V_{\mathrm {o}}=0 \ \mathrm {V} \ \)のときの時刻を\( \ t=T_{1}+T_{2} \ \mathrm {[s]} \ \)とすると,測定電圧は\( \ V_{\mathrm {x}}= \ \fbox { (ウ) } \ \mathrm {[V]} \ \)と表される。さらに,図2(c)のようにスイッチ\( \ \mathrm {S}_{1} \ \),\( \ \mathrm {S}_{2} \ \)の各期間\( \ T_{1} \ \mathrm {[s]} \ \),\( \ T_{2} \ \mathrm {[s]} \ \)中にクロックパルス発振器から出力されるクロックパルス数をそれぞれ\( \ N_{1} \ \),\( \ N_{2} \ \)とすると,\( \ N_{1} \ \)は既知なので\( \ N_{2} \ \)をカウントすれば,測定電圧\( \ V_{\mathrm {x}} \ \)がディジタル信号に変換される。ここで,クロックパルスの周期\( \ T_{\mathrm {s}} \ \)は,クロックパルス発振器の動作周波数に\( \ \fbox { (エ) } \ \)する。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & kV_{\mathrm {x}}T_{1} & kV_{\mathrm {r}}\left( t-T_{1}\right) & \displaystyle \frac {T_{2}}{T_{1}}V_{\mathrm {r}} & 反比例 \\
\hline
(2) & kV_{\mathrm {x}}T_{1} & kV_{\mathrm {r}}T_{2} & \displaystyle \frac {T_{2}}{T_{1}}V_{\mathrm {r}} & 反比例 \\
\hline
(3) & \displaystyle k\frac {V_{\mathrm {x}}}{T_{1}} & \displaystyle k\frac {V_{\mathrm {r}}}{T_{2}} & \displaystyle \frac {T_{1}}{T_{2}}V_{\mathrm {r}} & 比例 \\
\hline
(4) & \displaystyle k\frac {V_{\mathrm {x}}}{T_{1}} & \displaystyle k\frac {V_{\mathrm {r}}}{T_{2}} & \displaystyle \frac {T_{1}}{T_{2}}V_{\mathrm {r}} & 反比例 \\
\hline
(5) & kV_{\mathrm {x}}T_{1} & kV_{\mathrm {r}}\left( t-T_{1}\right) & T_{1}T_{2}V_{\mathrm {r}} & 比例 \\
\hline
\end{array}
\]
(b) 基準電圧が\( \ V_{\mathrm {r}}=2.0 \ \mathrm {V} \ \),スイッチ\( \ \mathrm {S}_{1} \ \)の期間\( \ T_{1} \ \mathrm {[s]} \ \)中のクロックパルス数が\( \ N_{1}=1.0\times 10^{3} \ \)のディジタル直流電圧計がある。この電圧計を用いて未知の電圧\( \ V_{\mathrm {x}} \ \mathrm {[V]} \ \)を測定したとき,スイッチ\( \ \mathrm {S}_{2} \ \)の期間\( \ T_{2} \ \mathrm {[s]} \ \)中のクロックパルス数が\( \ N_{2}=2.0\times 10^{3} \ \)であった。測定された電圧\( \ V_{\mathrm {x}} \ \)の値\( \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.5 \ \) (2) \( \ 1.0 \ \) (3) \( \ 2.0 \ \) (4) \( \ 4.0 \ \) (5) \( \ 8.0 \ \)
【ワンポイント解説】
文章読解力が求められる問題ですが,それほど多くの知識がなくても解ける問題となっています。B問題としては比較的易しい問題となるので,しっかりと文章を読解して完答できるようにして下さい。
【解答】
(a)解答:(1)
(ア)
題意より,時刻\( \ t_{1} \ \)における\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は,入力電圧\( \ V_{\mathrm {i}} \ \mathrm {[V]} \ \)の期間\( \ 0~t_{1} \ \mathrm {[s]} \ \)で囲われる面積\( \ S \ \)に比例するので,
\[
\begin{eqnarray}
V_{\mathrm {o}}(t_{1})&=&V_{\mathrm {x}}t_{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,積分器の特性で決まる比例定数\( \ k(>0) \ \)とすると,時刻\( \ t=T_{1} \ \mathrm {[s]} \ \)のときの出力電圧\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {m}}&=&kV_{\mathrm {x}}T_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(イ)
時刻\( \ t \ \)における\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は,\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)から\( \ -V_{\mathrm {r}}(V_{\mathrm {r}}>0) \ \mathrm {[V]} \ \)が\( \ T_{1}~t \ \mathrm {[s]} \ \)で囲われる面積を差し引いた大きさとなる。したがって,
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&V_{\mathrm {m}}-kV_{\mathrm {r}}\left( t-T_{1}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(ウ)
時刻\( \ t=T_{1}+T_{2} \ \mathrm {[s]} \ \)の時の電圧は,(ア),(イ)より,
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&V_{\mathrm {m}}-kV_{\mathrm {r}}\left( T_{1}+T_{2}-T_{1}\right) \\[ 5pt ]
&=&kV_{\mathrm {x}}T_{1}-kV_{\mathrm {r}}T_{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,この電圧が零となるので,
\[
\begin{eqnarray}
0&=&kV_{\mathrm {x}}T_{1}-kV_{\mathrm {r}}T_{2} \\[ 5pt ]
kV_{\mathrm {x}}T_{1}&=&kV_{\mathrm {r}}T_{2} \\[ 5pt ]
V_{\mathrm {x}}&=&\frac {T_{2}}{T_{1}}V_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(エ)
クロックパルスの周期\( \ T_{\mathrm {s}} \ \)は,クロックパルス発振器の動作周波数\( \ f \ \)とすると,
\[
\begin{eqnarray}
T_{\mathrm {s}}&=&\frac {1}{f} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,クロックパルスの周期\( \ T_{\mathrm {s}} \ \)は,クロックパルス発振器の動作周波数\( \ f \ \)に反比例する。
(b)解答:(4)
図2(c)より,
\[
\begin{eqnarray}
V_{\mathrm {x}}N_{1}&=&V_{\mathrm {r}}N_{2} \\[ 5pt ]
V_{\mathrm {x}}&=&\frac {N_{2}}{N_{1}}V_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,それぞれ値を代入すると,
\[
\begin{eqnarray}
V_{\mathrm {x}}&=&\frac {2.0\times 10^{3}}{1.0\times 10^{3}}\times 2.0 \\[ 5pt ]
&=&4.0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは