Contents
【問題】
【難易度】★★★☆☆(普通)
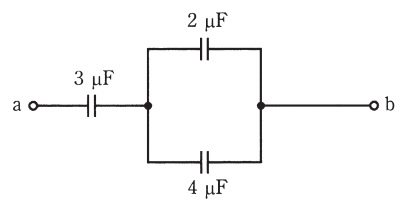
図のように,三つの平行平板コンデンサを直並列に接続した回路がある。ここで,それぞれのコンデンサの極板の形状及び面積は同じであり,極板間には同一の誘電体が満たされている。なお,コンデンサの初期電荷は零とし,端効果は無視できるものとする。
いま,端子\( \ \mathrm {a-b} \ \)間に直流電圧\( \ 300 \ \mathrm {[V]} \ \)を加えた。このとき,次の(a)及び(b)の問に答えよ。
(a) 静電容量が\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサに蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)の値として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1.2\times 10^{-4} \ \) (2) \( \ 2\times 10^{-4} \ \) (3) \( \ 2.4\times 10^{-4} \ \) (4) \( \ 3\times 10^{-4} \ \) (5) \( \ 4\times 10^{-4} \ \)
(b) 静電容量が\( \ 3 \ \mathrm {[\mu F ]} \ \)のコンデンサの極板間の電界の強さは,\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサの極板間の電界の強さの何倍か。倍率として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ \displaystyle \frac {3}{4} \ \) (2) \( \ 1.0 \ \) (3) \( \ \displaystyle \frac {4}{3} \ \) (4) \( \ \displaystyle \frac {3}{2} \ \) (5) \( \ 2.0 \ \)
【ワンポイント解説】
電磁気と電気回路の複合的な問題ですが,(a)は難易度は\( \ \mathrm {B} \ \)問題としては易しい部類に入ると思います。(b)はやや引っ掛け問題となっている印象があります。平行平板コンデンサの基本公式をきちんと思い出して,確実に解けるようにしましょう。
1.コンデンサの極板間に蓄えられる電荷\( \ Q \ \)
静電容量\( \ C \ \)のコンデンサに電圧\( \ V \ \)をかけて十分時間が経った時,コンデンサに蓄えられる電荷\( \ Q \ \)は,
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \),極板の面積を\( \ S \ \),極板間の距離を\( \ d \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \)と\( \ C_{2} \ \)の合成静電容量\( \ C \ \)は,
並列接続時:\( \ C=C_{1}+C_{2} \ \)
直列接続時:\( \ \displaystyle C=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ \)
となります。
4.平行平板コンデンサの極板間の電界\( \ E \ \)
極板間の距離\( \ d \ \)の平行平板コンデンサに,電圧\( \ V \ \)の電源を接続すると,極板間の電界\( \ E \ \)は,
\[
\begin{eqnarray}
E &=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(5)
\( \ 2 \ \mathrm {[\mu F ]} \ \)と\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサの合成静電容量は,ワンポイント解説「3.コンデンサの合成静電容量」より,
\[
\begin{eqnarray}
2 +4&=&6 \ \mathrm {[\mu F]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,回路は図1のように書き換えられる。
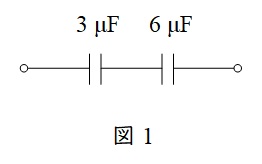
図1において\( \ \mathrm {a-b} \ \)間に電圧をかけた時,\( \ 3 \ \mathrm {[\mu F ]} \ \)と\( \ 6 \ \mathrm {[\mu F ]} \ \)のコンデンサに蓄えられる電荷は等しいので,蓄えられる電荷を\( \ Q_{0} \ \),\( \ 3 \ \mathrm {[\mu F ]} \ \)のコンデンサにかかる電圧を\( \ V_{1} \ \),\( \ 6 \ \mathrm {[\mu F ]} \ \)のコンデンサにかかる電圧を\( \ V_{2} \ \)とすると,
\[
\begin{eqnarray}
V_{1}&=&\frac {Q_{0}}{3\times 10^{-6}} \\[ 5pt ]
V_{2}&=&\frac {Q_{0}}{6\times 10^{-6}} \\[ 5pt ]
\end{eqnarray}
\]
なので,
\[
\begin{eqnarray}
V_{1}&=&2V_{2} ・・・・・・・・ ①\\[ 5pt ]
\end{eqnarray}
\]
となる。また,題意より,
\[
\begin{eqnarray}
V_{1}+V_{2}&=&300 \ ・・・・・ ②\\[ 5pt ]
\end{eqnarray}
\]
なので,①,②を解くと,
\[
\begin{eqnarray}
V_{1}&=&200 \ \mathrm {[V]} \\[ 5pt ]
V_{2}&=&100 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ V_{2} \ \)は\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサにかかる電圧なので,\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサに蓄えられる電荷\( \ Q \ \)は,
\[
\begin{eqnarray}
Q &=&4\times 10^{-6}\times 100 \\[ 5pt ]
&=&4\times 10^{-4} \ \mathrm {[C]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
\( \ 3 \ \mathrm {[\mu F ]} \ \)のコンデンサの極板間の距離を\( \ d_{1} \ \)及び\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサの極板間の距離を\( \ d_{2} \ \)とすると,誘電率及び面積は等しいので,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」より,
\[
\begin{eqnarray}
3\times 10^{-6} &=&\frac {\varepsilon S}{d_{1}} \\[ 5pt ]
d_{1}&=&\frac {\varepsilon S}{3\times 10^{-6}} \\[ 5pt ]
4\times 10^{-6} &=&\frac {\varepsilon S}{d_{2}} \\[ 5pt ]
d_{2}&=&\frac {\varepsilon S}{4\times 10^{-6}} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ 3 \ \mathrm {[\mu F ]} \ \)のコンデンサの電界\( \ E_{1} \ \)及び\( \ 4 \ \mathrm {[\mu F ]} \ \)のコンデンサの電界\( \ E_{2} \ \)は,極板間の距離を\( \ d \ \)とすると,ワンポイント解説「4.平行平板コンデンサの極板間の電界\( \ E \ \)」より,
\[
\begin{eqnarray}
E_{1} &=&\frac {V_{1}}{d_{1}} \\[ 5pt ]
&=&\frac {200}{\displaystyle \frac {\varepsilon S}{3\times 10^{-6}}} \\[ 5pt ]
&=&\frac {6\times 10^{-4}}{\varepsilon S} \\[ 5pt ]
E_{2} &=&\frac {V_{2}}{d_{2}} \\[ 5pt ]
&=&\frac {100}{\displaystyle \frac {\varepsilon S}{4\times 10^{-6}}} \\[ 5pt ]
&=&\frac {4\times 10^{-4}}{\varepsilon S} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ E_{1}=\displaystyle \frac {3}{2}E_{2} \ \)すなわち\( \displaystyle \frac {3}{2} \ \)倍と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは