《理論》〈電子理論〉[H30:問12]磁界中の電子の運動に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，磁界中の電子の運動に関する記述である。

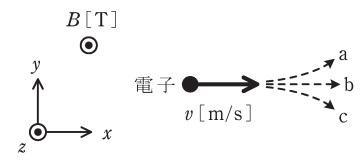
図のように，平等磁界の存在する真空かつ無重力の空間に，電子を$\ x \ $方向に初速度$\ v \ \mathrm {[ m ／ s ]} \ $で放出する。平等磁界は$\ z \ $方向であり磁束密度の大きさ$\ B \ \mathrm {[ T ]} \ $をもつとし，電子の質量を$\ m \ \mathrm {[ kg ]} \ $，素電荷の大きさを$\ e \ \mathrm {[ C ]} \ $とする。ただし，紙面の裏側から表側への向きを$\ z \ $方向の正とし，$\ v \ $は光速に比べて十分小さいとする。このとき，電子の運動は$\fbox {　 （ア） 　}$となり，時間$\ T=\fbox {　 （イ） 　} \ \mathrm {[ s ]} \ $後に元の位置に戻ってくる。電子の放出直後の軌跡は破線矢印の$\fbox {　 （ウ） 　}$のようになる。

一方，電子を磁界と平行な$\ z \ $方向に放出すると，電子の運動は$\fbox {　 （エ） 　}$となる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

$$\begin{array}{ccccc} & （ア） & （イ） & （ウ） & （エ） \\ \hline (1) & 単振動 & \displaystyle \frac {m}{eB} & \mathrm {a} & 等加速度運動 \\ \hline (2) & 単振動 & \displaystyle \frac {m}{2\pi eB} & \mathrm {b} & らせん運動 \\ \hline (3) & 等速円運動 & \displaystyle \frac {m}{eB} & \mathrm {c} & 等速直線運動 \\ \hline (4) & 等速円運動 & \displaystyle \frac {2\pi m}{eB} & \mathrm {c} & らせん運動 \\ \hline (5) & 等速円運動 & \displaystyle \frac {2\pi m}{eB} & \mathrm {a} & 等速直線運動 \\ \hline \end{array}$$

【ワンポイント解説】

(イ)の導出が本問の肝となるので，(イ)が自力で導出できるようにしましょう。ただ，本問の場合は(イ)が導出できなくてもフレミングの左手の法則を理解していれば解けてしまうので問題としては易しめの問題となります。

【解答】

解答：(5)
(ア)
本問のような条件では電子はすべて回転円の中心に向かう力が加わり，等速円運動となります。

(イ)
与えられた条件において，電子に加わる電磁力$F$は，
$$\begin{eqnarray} F &=&evB \\[ 5pt ] \end{eqnarray}$$ であり，向心力$F$
$$\begin{eqnarray} F &=&\frac {mv^{2}}{r} \\[ 5pt ] \end{eqnarray}$$ と等しいから，
$$\begin{eqnarray} evB &=&\frac {mv^{2}}{r} \\[ 5pt ] r &=&\frac {mv}{eB} \\[ 5pt ] \end{eqnarray}$$ の等速円運動となる。電子が元の位置に戻ってくる時間$T$は，
$$\begin{eqnarray} T &=&\frac {2\pi r}{v} \\[ 5pt ] &=&\frac {2\pi }{v}\cdot \frac {mv}{eB} \\[ 5pt ] &=&\frac {2\pi m}{eB} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(ウ)
フレミングの左手の法則より，電流の向き(中指)が$-x$方向，磁界の向き(人差し指)が$z$方向であるから，力の向き(親指)は$y$方向となります。よって，電子は$a$方向に動きます。

(エ)
電子を$\ z \ $方向に放出すると，電子には一切力が加わらないため，電子は等速直線運動をすることになります。