《理論》〈電気及び電子計測〉[H25:問16]オシロスコープの観測結果からの考察に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

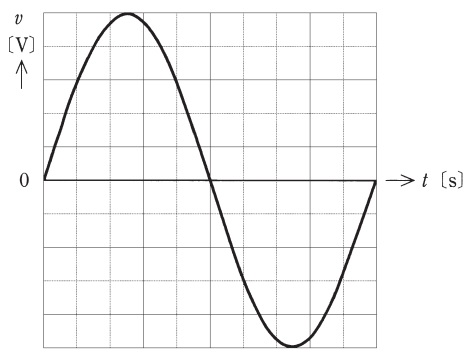
振幅\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)の交流電源の電圧\( \ v=V_{\mathrm {m}}\sin \omega t \ \mathrm {[V]} \ \)をオシロスコープで計測したところ，画面上に図のような正弦波形が観測された。次の(a)及び(b)の問に答えよ。

ただし，オシロスコープの垂直感度は幅\( \ 5 \ \mathrm {[V]}／\mathrm {div} \ \)，掃引時間は\( \ 2 \ \mathrm {[ms]}／\mathrm {div} \ \)とし，測定に用いたプローブの減衰比は\( \ 1 \ \)対\( \ 1 \ \)とする。

(a)　この交流電源の電圧の周期\( \ \mathrm {[ms]} \ \)，周波数\( \ \mathrm {[Hz]} \ \)，実効値\( \ \mathrm {[V]} \ \)の値の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& 　周　期　 & 　周波数　 & 　実効値　 \\
\hline
(1) & 20 & 50 & 15.9 \\
\hline
(2) & 10 & 100 & 25.0 \\
\hline
(3) & 20 & 50 & 17.7 \\
\hline
(4) & 10 & 100 & 17.7 \\
\hline
(5) & 20 & 50 & 25.0 \\
\hline
\end{array}
\]

(b)　この交流電源をある負荷に接続したとき，\( \ i=25\cos \left( \omega t-\displaystyle \frac {\pi }{3}\right) \ \mathrm {[A]} \ \)の電流が流れた。この負荷の力率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(50\)　　(2)　\(60\)　　(3)　\(70.7\)　　(4)　\(86.6\)　　(5)　\(100\)

【ワンポイント解説】

オシロスコープの測定結果から各値を導出する問題で，計算の難易度としては比較的易しい内容となっています。(b)の\( \ \cos \ \)から\( \ \sin \ \)への変換はそれぞれの分かりやすい点の関係から理解すると良いと思います。

　例：\( \ \displaystyle \sin \frac {\pi }{2}=\cos 0 \ \)なので\( \ \displaystyle \sin \left( \delta +\frac {\pi }{2}\right) =\cos \delta \ \)となる。

【解答】

(a)解答：(3)
題意より，縦\( \ 1 \ \)マスの大きさは\( \ 5 \ \mathrm {V} \ \)，横\( \ 1 \ \)マスの大きさは\( \ 2 \ \mathrm {ms} \ \)であるから，測定結果の振幅\( \ V_{\mathrm {m}} \ \)は\( \ 20 \ \mathrm {V} \ \)，周期\( \ T \ \)は\( \ 20 \ \mathrm {ms} \ \)となる。
よって，周波数\( \ f \ \mathrm {[Hz]} \ \)は，
\[
\begin{eqnarray}
f&=&\frac {1}{T} \\[ 5pt ] &=&\frac {1}{20\times 10^{-3}} \\[ 5pt ] &=&50 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められ，実効値\( \ V \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V&=&\frac {V_{\mathrm {m}}}{\sqrt {2}} \\[ 5pt ] &=&\frac {25}{\sqrt {2}} \\[ 5pt ] &≒&17.7 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
オシロスコープの測定結果より，\( \ v=25\sin \omega t \ \mathrm {[V]} \ \)である。
また，\( \ \displaystyle \sin \left( \delta +\frac {\pi }{2}\right) =\cos \delta \ \)の関係性から，
\[
\begin{eqnarray}
i&=&25\cos \left( \omega t-\displaystyle \frac {\pi }{3}\right) \\[ 5pt ] &=&25\sin \left( \omega t-\displaystyle \frac {\pi }{3}+\frac {\pi }{2}\right) \\[ 5pt ] &=&25\sin \left( \omega t+\frac {\pi }{6}\right) \\[ 5pt ] \end{eqnarray}
\] となり，電流は電圧より\( \ \displaystyle \frac {\pi }{6} \ \)だけ進んでいることになる。したがって，力率\( \ \cos \theta \ \)は，
\[
\begin{eqnarray}
\cos \theta &=&\cos \frac {\pi }{6} \\[ 5pt ] &=&\frac {\sqrt {3}}{2} \\[ 5pt ] &≒&0.866　→　86.6 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。