Contents
【問題】
【難易度】★★★☆☆(普通)
磁界及び磁束に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1 \ \mathrm {[m]} \ \)当たりの巻数が\( \ N \ \)の無限に長いソレノイドに電流\( \ I \ \mathrm {[A]} \ \)を流すと,ソレノイドの内部には磁界\( \ H=NI \ \mathrm {[A/m]} \ \)が生じる。磁界の大きさは,ソレノイドの寸法や内部に存在する物質の種類に影響されない。
(2) 均一磁界中において,磁界の方向と直角に置かれた直線状導体に直流電流を流すと,導体には電流の大きさに比例した力が働く。
(3) \( \ 2 \ \)本の平行な直線状導体に反対向きの電流を流すと,導体には導体間距離の\( \ 2 \ \)乗に反比例した反発力が働く。
(4) フレミングの左手の法則では,親指の向きが導体に働く力の向きを示す。
(5) 磁気回路において,透磁率は電気回路の導電率に,磁束は電気回路の電流にそれぞれ対応する。
【ワンポイント解説】
諸々の基本公式をきちんと理解しているかを問う問題です。誤答選択問題ですが,実際には自分で作図・計算をして式を導出できるようになるための計算能力が必要となります。
1.アンペアの周回積分の法則
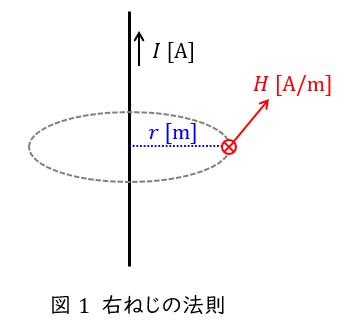
電流\( \ I \ \mathrm {[A]} \ \)の流れる向きに右ねじを合わせる(図1においては上向き)と,右ねじを回す向きに磁界\( \ H \ \mathrm {[A / m ]} \ \)が発生し,距離\( \ r \ \mathrm {[m]} \ \)離れた場所の磁界の大きさは,
\[
\begin{eqnarray}
H &=&\frac {I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.フレミングの左手の法則
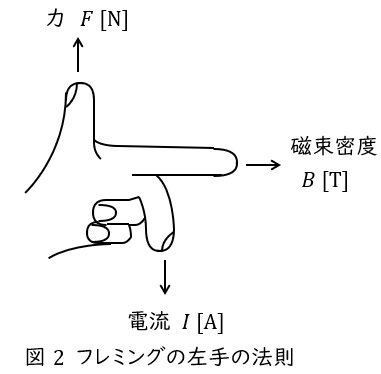
中指を電流の向き,人差し指を磁界の向きに合わせると,親指の方向に力が働くという法則で,頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \),電流の大きさ\( \ I \ \mathrm {[A]} \ \),直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると,導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.無限長ソレノイドの内部に発生する磁界
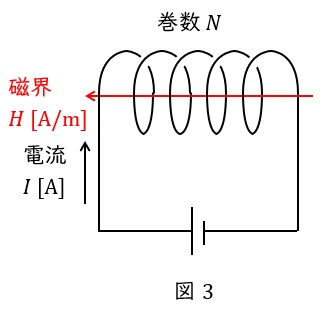
図3に示すような単位長さ当たりの巻数\( \ N \ \)のソレノイド(長さは無限長とします)の内部に発生する磁界の大きさ\( \ H \ \mathrm {[A / m ]} \ \)は,
\[
\begin{eqnarray}
H &=&NI \\[ 5pt ]
\end{eqnarray}
\]
となります。
計算で導出するためには,ビオサバールの法則と積分を使用するため,覚えておく必要があります。
4.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係
磁束密度\( \ B \ \mathrm {[T]} \ \)と磁界の大きさ\( \ H \ \mathrm {[A / m ]} \ \)には,透磁率を\( \ \mu \ \mathrm {[H / m ]} \ \)とすると,
\[
\begin{eqnarray}
B &=&\mu H \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
解答:(3)
(1)正しい
ワンポイント解説「3.無限長ソレノイドの内部に発生する磁界」の通り,ソレノイドの内部には\( \ H=NI \ \mathrm {[A/m]} \ \)の磁界が生じます。また,磁界の大きさは,巻数\( \ N \ \)や電流\( \ I \ \mathrm {[A]} \ \)以外のソレノイドの寸法や内部に存在する物質の種類に影響されません。
(2)正しい
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \),電流の大きさ\( \ I \ \mathrm {[A]} \ \),直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると,導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ]
\end{eqnarray}
\]
となり,電流の大きさに比例した力が働きます。
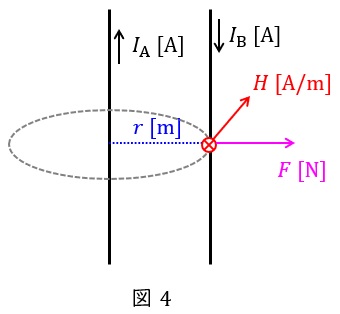
(3)誤り
図4のような距離\( \ r \ \mathrm {[m]} \ \)離れた反対向きに電流を流した例で考えます。\( \ I_{\mathrm {A}} \ \)が導体\( \ \mathrm {B} \ \)上に発生する磁界の大きさ\( \ H \ \mathrm {[A / m ]} \ \)は,
\[
\begin{eqnarray}
H &=&\frac {I_{\mathrm {A}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)は透磁率を\( \ \mu \ \mathrm {[H / m ]} \ \)とすると,ワンポイント解説「4.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」より,
\[
\begin{eqnarray}
B &=&\mu H \\[ 5pt ]
&=&\frac {\mu I_{\mathrm {A}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。ワンポイント解説「2.フレミングの左手の法則」より,中指を電流の向き,人差し指を磁界の向きに合わせると,親指の方向は反発する方向に働き,その単位長さ当たりの大きさ\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&BI_{\mathrm {B}}\times 1 \\[ 5pt ]
&=&\frac {\mu I_{\mathrm {A}}I_{\mathrm {B}}}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,導体間距離\( \ r \ \)に反比例した大きさの反発力が発生します。この式は公式として紹介されている参考書もあるので,覚えておいても良い式となります。
(4)正しい
ワンポイント解説「2.フレミングの左手の法則」の通り,親指の向きが導体に働く力の向きとなります。
(5)正しい
磁気回路においては,起磁力\( \ F=NI \ \mathrm {[A]} \ \),磁束\( \ \mathit {\phi } \ \mathrm {[Wb]} \ \),磁気抵抗\( \ \displaystyle R_{\mathrm {m}}=\frac {l}{\mu S} \ \mathrm {[H^{-1}]} \ \)とすると,
\[
\begin{eqnarray}
F &=&\mathit {\phi }R_{\mathrm {m}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,透磁率は電気回路の導電率に,磁束は電気回路の電流にそれぞれ対応します。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは