《理論》〈電気回路〉[H29:問8]交流回路の回路計算に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

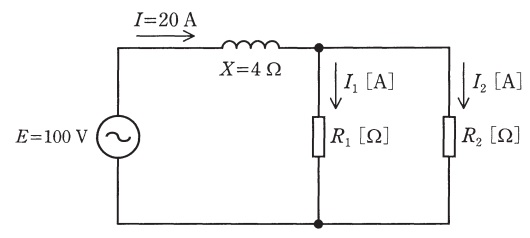
図のように，交流電圧\( \ E=100 \ \mathrm {V} \ \)の電源，誘導性リアクタンス\( \ X=4 \ \Omega \ \)のコイル，\( \ R_{1} \ \left[ \Omega \right] \ \)，\( \ R_{2} \ \left[ \Omega \right] \ \)の抵抗からなる回路がある。いま，回路を流れる電流の値が\( \ I=20 \ \mathrm {A} \ \)であり，また，抵抗\( \ R_{1} \ \)に流れる電流\( \ I_{1} \ \left[ \mathrm {A}\right] \ \)と抵抗\( \ R_{2} \ \)に流れる電流\( \ I_{2} \ \left[ \mathrm {A}\right] \ \)との比が，\( \ I_{1}:I_{2}=1:3 \ \)であった。この時，抵抗\( \ R_{1} \ \)の値\( \ \left[ \Omega \right] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(1.0\)　　(2)　\(3.0\)　　(3)　\(4.0\)　　(4)　\(9.0\)　　(5)　\(12\)

【ワンポイント解説】

交流回路ではリアクトルとコンデンサで電圧と電流に\( \ 90° \ \)の位相差が発生します。したがって，回路計算する際は，ベクトル図を書くとわかりやすくなると思います。

1.並列回路の合成抵抗
\( \ R_{1} \ \)と\( \ R_{2} \ \)の並列回路の合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] すなわち，
\[
\begin{eqnarray}
R&=&\frac{R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.交流回路における抵抗とリアクトルの特性
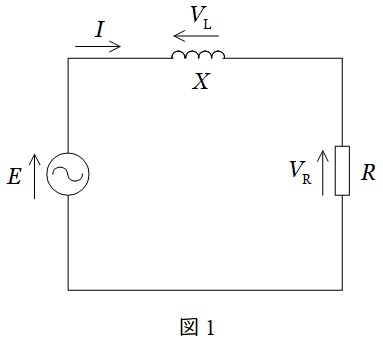
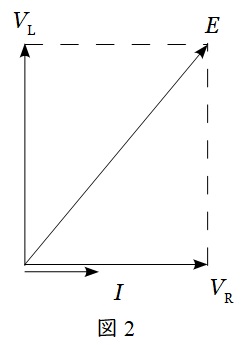
図1の回路において電源の電圧を\( \ E \ \)，リアクトル\( \ X \ \)と抵抗\( \ R \ \)に流れる電流を\( \ I \ \)とすると，リアクトルは電流が電圧より\( \ 90° \ \)遅れるため，ベクトル図は図2のように描けます。この時，
\[
\begin{eqnarray}
V_{\mathrm {L}}&=&XI，V_{\mathrm {R}}&=&RI \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
E&=&\sqrt {V_{\mathrm {L}}^{2}+V_{\mathrm {R}}^{2}} \\[ 5pt ] &=&\sqrt {\left( XI\right) ^{2}+\left( RI\right) ^{2}} \\[ 5pt ] &=&\sqrt {X^{2}+R^{2}}I \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(5)
題意より，\( \ I_{1}:I_{2}=1:3 \ \)であり，
\[
\begin{eqnarray}
R_{1}I_{1}&=&R_{2}I_{2} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
R_{1}I_{1}&=&R_{2}\times 3I_{1} \\[ 5pt ] R_{1}&=&3R_{2} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ R_{1} \ \)と\( \ R_{2} \ \)の並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R &=& \frac{R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] &=& \frac{3R_{2}\cdot R_{2}}{3R_{2}+R_{2}} \\[ 5pt ] &=& \frac {3}{4}R_{2} \\[ 5pt ] &=& \frac {R_{1}}{4}
\end{eqnarray}
\] となる。ワンポイント解説「2.交流回路における抵抗とリアクトルの特性」より，
\[
\begin{eqnarray}
E &=& \sqrt {X^{2}+R^{2}}I \\[ 5pt ] 100 &=& \sqrt {4^{2}+R^{2}}\times 20 \\[ 5pt ] 5 &=& \sqrt {4^{2}+R^{2}} \\[ 5pt ] 25 &=& 4^{2}+R^{2} \\[ 5pt ] R^{2}&=& 9 \\[ 5pt ] R &=& 3
\end{eqnarray}
\] となる。ゆえに，
\[
\begin{eqnarray}
R_{1}&=&4R \\[ 5pt ] &=&4\times 3 \\[ 5pt ] &=&12 \ \left[ \Omega \right] \\[ 5pt ] \end{eqnarray}
\] と求められる。