《理論》〈電磁気〉[R4上:問2]クーロンの法則による点電荷に加わる力の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

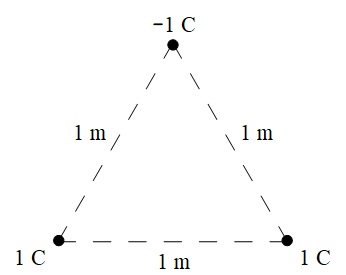
真空中において，図に示すように一辺の長さが\( \ 1 \ \mathrm {m} \ \)の正三角形の各頂点に\( \ 1 \ \mathrm {C} \ \)又は\( \ -1 \ \mathrm {C} \ \)の点電荷がある。この場合，正の点電荷に働く力の大きさ\( \ F_{1} \ \mathrm {[N]} \ \)と，負の点電荷に働く力の大きさ\( \ F_{2} \ \mathrm {[N]} \ \)の比\( \ F_{2} ／ F_{1} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \sqrt {2} \ \)　　(2)　\( \ 1.5 \ \)　　(3)　\( \ \sqrt {3} \ \)　　(4)　\( \ 2 \ \)　　(5)　\( \ \sqrt {5} \ \)　　

【ワンポイント解説】

クーロンの法則を用いた点電荷に加わる力の導出に関する問題です。
クーロンの法則は多くの参考書の最初に出てくる公式なので，多くの受験生が正答できた問題であるかと思います。
各電荷に加わる力の作図を丁寧に行い，ミスの出ないように注意して解くようにして下さい。

1.クーロンの法則
真空中で距離\( \ r \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \)，\( \ Q_{\mathrm {B}} \ \)に加わる力\( \ F \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \)とすると，
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。このとき，\( \ Q_{\mathrm {A}} \ \)，\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力（反発する力），異符号である場合には引力（引き合う力）が働きます。

【解答】

解答：(3)
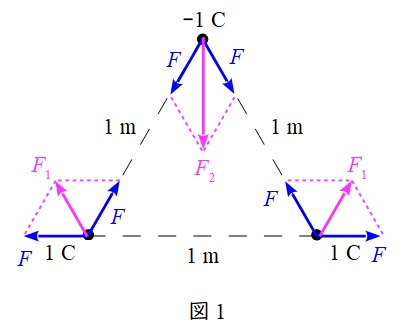
各電荷に加わる力を図に示すと図1のようになる。
図1において各電荷間に加わる力の大きさ\( \ F \ \mathrm {[N]} \ \)は，ワンポイント解説「1.クーロンの法則」より，
\[
\begin{eqnarray}
F &=&\frac {1\times 1}{4\pi \varepsilon _{0}\times 1^{2}} \\[ 5pt ] &=&\frac {1}{4\pi \varepsilon _{0}} \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となり，すべて等しい。
図1より，\( \ 1 \ \mathrm {C} \ \)の電荷に加わる力は\( \ F \ \mathrm {[N]} \ \)と等しいため，\( \ F_{1}=F \ \mathrm {[N]} \ \)となる。
また，\( \ -1 \ \mathrm {C} \ \)の電荷に加わる力は正三角形の性質より，
\[
\begin{eqnarray}
F_{2} &=&\frac {\sqrt {3}}{2}F\cdot 2 \\[ 5pt ] &=&\sqrt {3}F \ \mathrm {[N]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ F_{1} \ \mathrm {[N]} \ \)と\( \ F_{2} \ \mathrm {[N]} \ \)の比\( \ F_{2} ／ F_{1} \ \)は，
\[
\begin{eqnarray}
\frac {F_{2}}{F_{1}} &=&\frac {\sqrt {3}F}{F} \\[ 5pt ] &=&\sqrt {3} \\[ 5pt ] \end{eqnarray}
\] と求められる。