【問題】
【難易度】★★★☆☆(普通)
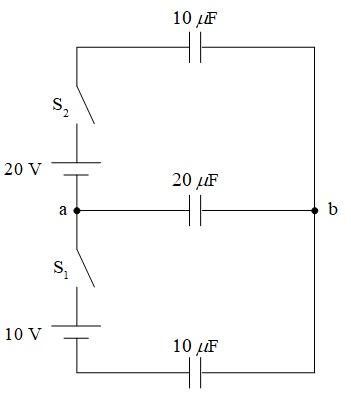
図のように,コンデンサ3個を充電する回路がある。スイッチ\(\mathrm {S}_{1}\)及び\(\mathrm {S}_{2}\)を同時に閉じてから十分に時間が経過し,定常状態となったとき,\(\mathrm {a}\)点からみた\(\mathrm {b}\)点の電圧の値\(\mathrm {[V]}\)として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,各コンデンサの初期負荷は零とする。
(1) \(\displaystyle -\frac {10}{3}\) (2) \(-2.5\) (3) \(2.5\) (4) \(\displaystyle \frac {10}{3}\) (5) \(\displaystyle \frac {20}{3}\)
【ワンポイント解説】
普通に解いても解ける問題ですが,本問では重ね合わせの理を用いるのが最も楽な方法であると思います。
1.重ね合わせの理
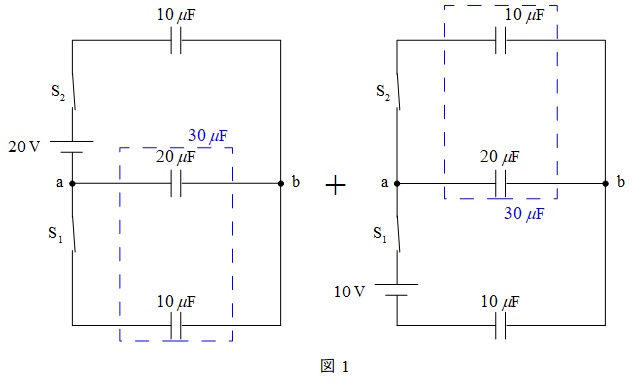
複数の電源で構成された回路は,電源毎に計算した電流を重ね合わせて求めることができます。この時,電圧源は短絡,電流源は開放します。本問の回路は図1のように分解できます。
2.コンデンサの分圧
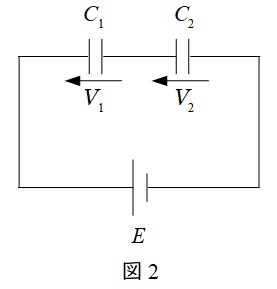
図2の回路において,各コンデンサに蓄えられる電荷が等しいので,
\[
C_{1}V_{1}=C_{2}V_{2} ・・・・・・・①
\]
となり,\(V_{1}\)と\(V_{2}\)の合計が電源電圧と等しいので,
\[
V_{1}+V_{2}=E ・・・・・・・②
\]
となります。②より,
\[
V_{2}=E-V_{1}
\]
であるので,これを①に代入すると,
\[
\begin{eqnarray}
C_{1}V_{1}&=&C_{2}\left( E-V_{1}\right) \\[ 5pt ]
\left( C_{1}+C_{2}\right) V_{1}&=&C_{2}E \\[ 5pt ]
V_{1}&=&\frac {C_{2}}{C_{1}+C_{2}}E \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に,
\[
V_{2}=\frac {C_{1}}{C_{1}+C_{2}}E
\]
と求められます。
【関連する「電気の神髄」記事】
【解答】
解答:(3)
ワンポイント解説「1.重ね合わせの理」の通り,問題図は図1のように分解できる。図1左において□で囲んだ部分の並列合成静電容量は\(30 \ \mathrm {\mu F}\)であるから,\(\mathrm {a}\)点からみた\(\mathrm {b}\)点の電圧\(V_{\mathrm {ba1}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {ba1}}&=&\frac {10}{10+30}\times 20 \\[ 5pt ]
&=&5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に図1右において\(\mathrm {a}\)点からみた\(\mathrm {b}\)点の電圧\(V_{\mathrm {ba2}}\)は,電圧の向きに注意すると,
\[
\begin{eqnarray}
-V_{\mathrm {ba2}}&=&\frac {10}{10+30}\times 10 \\[ 5pt ]
V_{\mathrm {ba2}}&=&-2.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\(\mathrm {a}\)点からみた\(\mathrm {b}\)点の電圧はそれぞれの電圧の合成であるから,
\[
\begin{eqnarray}
V_{\mathrm {ba}}&=&V_{\mathrm {ba1}}+V_{\mathrm {ba2}} \\[ 5pt ]
&=&5-2.5 \\[ 5pt ]
&=&2.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは