《理論》〈電気及び電子計測〉[R4下:問16]内部抵抗の異なる二つの電流計の並列接続に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

最大目盛\( \ 50 \ \mathrm {A} \ \)，内部抵抗\( \ 0.8\times 10^{-3} \ \mathrm {\Omega } \ \)の直流電流計\( \ \mathrm {A_{1}} \ \)と最大目盛\( \ 100 \ \mathrm {A} \ \)，内部抵抗\( \ 0.32\times 10^{-3} \ \mathrm {\Omega } \ \)の直流電流計\( \ \mathrm {A_{2}} \ \)の二つの直流電流計がある。次の(a)及び(b)の問に答えよ。

ただし，二つの直流電流計は直読式指示電気計器であるとし，固有誤差はないものとする。

(a)　二つの直流電流計を並列に接続して使用したとき，測定できる電流の最大の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 40 \ \)　　(2)　\( \ 50 \ \)　　(3)　\( \ 100 \ \)　　(4)　\( \ 132 \ \)　　(5)　\( \ 140 \ \)

(b)　小問(a)での接続を基にして，直流電流\( \ 150 \ \mathrm {A} \ \)の電流を測定するために，二つの直流電流計の指示を最大目盛にして測定したい。そのためには，直流電流計\( \ \mathrm {A_{2}} \ \)に抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を直列に接続することで，各直流電流計の指示を最大目盛にして測定することができる。抵抗\( \ R \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3.2\times 10^{-5} \ \)　　(2)　\( \ 5.6\times 10^{-5} \ \)　　(3)　\( \ 8\times 10^{-5} \ \)　
　(4)　\( \ 11.2\times 10^{-5} \ \)　　(5)　\( \ 13.6\times 10^{-5} \ \)

【ワンポイント解説】

最大目盛と内部抵抗の異なる直流電流計の並列接続に関する問題です。
図が与えられていないため，読解力が求められる問題ですが，理解できればそれほど難しい公式を使用しないため完答できる問題となります。
差がつきやすい問題で，合格に向けてはできれば完答しておきたい問題です。

1.分圧・分流の法則
①分圧の法則
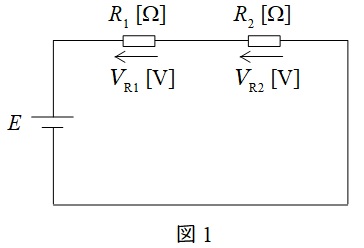
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
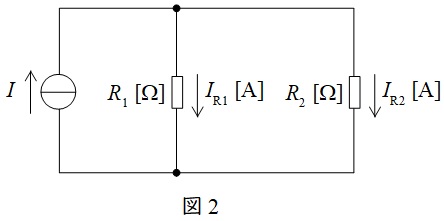
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(5)
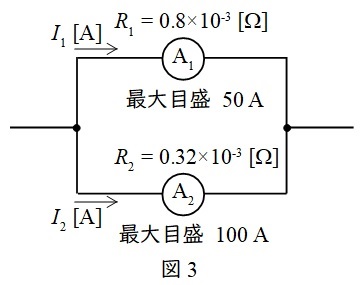
問題に沿って図を描くと図3のようになる。
図3において，分流の法則より，各電流計に流れる電流の比は抵抗の逆比となるから，
\[
\begin{eqnarray}
I_{\mathrm {1}}：I_{\mathrm {2}}&=&R_{2}：R_{1} \\[ 5pt ] &=&\left( 0.32\times 10^{-3}\right) ：\left( 0.8\times 10^{-3}\right) \\[ 5pt ] &=&0.32：0.8 \\[ 5pt ] &=&2：5 \\[ 5pt ] \end{eqnarray}
\] となるので，先に最大目盛に到達するのは電流計\( \ \mathrm {A_{2}} \ \)である。よって，\( \ I_{2}=100 \ \mathrm {[A]} \ \)のとき\( \ I_{1}=40 \ \mathrm {[A]} \ \)であるため，測定できる電流の最大値は\( \ I_{1}+I_{2}=140 \ \mathrm {[A]} \ \)と求められる。

(b)解答：(3)
二つの直流電流計を最大目盛にするためには，電流比\( \ I_{\mathrm {1}}：I_{\mathrm {2}} \ \)が\( \ 1：2 \ \)でなければならない。したがって，その時の抵抗値の比は\( \ 2：1 \ \)となる必要があるため，
\[
\begin{eqnarray}
\frac {R_{1}}{R_{2}+R}&=&2 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R \ \)について整理して各値を代入すると，
\[
\begin{eqnarray}
\frac {R_{1}}{2}&=&R_{2}+R \\[ 5pt ] R&=&\frac {R_{1}}{2}-R_{2} \\[ 5pt ] &=&\frac {0.8\times 10^{-3}}{2}-0.32\times 10^{-3} \\[ 5pt ] &=&0.08\times 10^{-3} \\[ 5pt ] &=&8\times 10^{-5} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。