《理論》〈電気回路〉[H24:問10]交流回路の電流比に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

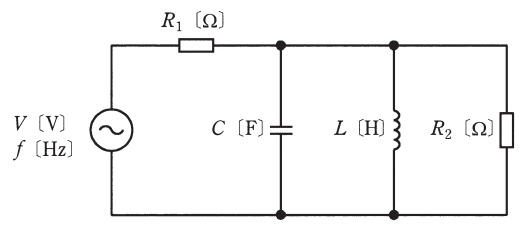
図のように，\( \ R_{1}=20 \ \mathrm {[\Omega ]} \ \)と\( \ R_{2}=30 \ \mathrm {[\Omega ]} \ \)の抵抗，静電容量\( \ \displaystyle C=\frac {1}{100\pi } \ \mathrm {[F]} \ \)のコンデンサ，インダクタンス\( \ \displaystyle L=\frac {1}{4\pi } \ \mathrm {[H]} \ \)のコイルからなる回路に周波数\( \ f \ \mathrm {[Hz]} \ \)で実効値\( \ V \ \mathrm {[V]} \ \)が一定の交流電圧を加えた。\( \ f=10 \ \mathrm {[Hz]} \ \)のときに\( \ R_{1} \ \)を流れる電流の大きさを\( \ I_{\mathrm {10Hz}} \ \mathrm {[A]} \ \)，\( \ f=10 \ \mathrm {[MHz]} \ \)のときに\( \ R_{1} \ \)を流れる電流の大きさを\( \ I_{\mathrm {10MHz}} \ \mathrm {[A]} \ \)とする。このとき，電流比\( \ \displaystyle \frac {I_{\mathrm {10Hz}}}{I_{\mathrm {10MHz}}} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.4 \ \)　　(2)　\( \ 0.6 \ \)　　(3)　\( \ 1.0 \ \)　　(4)　\( \ 1.7 \ \)　　(5)　\( \ 2.5 \ \)

【ワンポイント解説】

特別難しい公式を使用しませんが，\( \ f=10 \ \mathrm {[MHz]} \ \)のときの取扱いをどうするかが問われている問題であると思います。\( \ f=10 \ \mathrm {[MHz]} \ \)のときのコンデンサのリアクタンス\( \ \displaystyle \frac {1}{2\pi f C} \ \)が十分に小さくなることを念頭において解くようにしましょう。

【関連する「電気の神髄」記事】

　　並列共振回路の理論

【解答】

解答：(1)
\( \ f=10 \ \mathrm {[Hz]} \ \)の時のコンデンサ及びコイルのリアクタンス\( \ X_{\mathrm {C10Hz}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {L10Hz}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
-\mathrm {j}X_{\mathrm {C10Hz}} &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] &=&\frac {1}{\displaystyle \mathrm {j}2\pi \times 10 \times \frac {1}{100\pi }} \\[ 5pt ] &=&-\mathrm {j}5 \ \mathrm {[\Omega ]} \\[ 5pt ] \mathrm {j}X_{\mathrm {L10Hz}} &=&\mathrm {j}2\pi f L \\[ 5pt ] &=&\mathrm {j}2\pi \times 10 \times \frac {1}{4\pi } \\[ 5pt ] &=&\mathrm {j}5 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，合成リアクタンス\( \ \mathrm {j}X_{\mathrm {CL10Hz}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {CL10Hz}} &=&\frac {-\mathrm {j}X_{\mathrm {C10Hz}}\mathrm {j}X_{\mathrm {L10Hz}}}{-\mathrm {j}X_{\mathrm {C10Hz}}+\mathrm {j}X_{\mathrm {L10Hz}}} \\[ 5pt ] &=&\frac {-\mathrm {j}5\times \mathrm {j}5}{-\mathrm {j}5+\mathrm {j}5} \\[ 5pt ] &=&\frac {25}{0} \\[ 5pt ] &=&\infty \\[ 5pt ] \end{eqnarray}
\] となり，この回路は並列共振，すなわちコンデンサ及びコイルには電流が流れないことが分かる。したがって，\( \ f=10 \ \mathrm {[Hz]} \ \)のときに\( \ R_{1} \ \)を流れる電流の大きさ\( \ I_{\mathrm {10Hz}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {10Hz}} &=&\frac {V}{R_{1}+R_{2}} \\[ 5pt ] &=&\frac {V}{20+30} \\[ 5pt ] &=&\frac {V}{50} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。一方，\( \ f=10 \ \mathrm {[MHz]} \ \)の時のコンデンサ及びコイルのリアクタンス\( \ X_{\mathrm {C10MHz}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {L10MHz}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
-\mathrm {j}X_{\mathrm {C10MHz}} &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] &=&\frac {1}{\displaystyle \mathrm {j}2\pi \times 10 \times 10^{6} \times \frac {1}{100\pi }} \\[ 5pt ] &=&-\mathrm {j}5\times 10^{-6} \ \mathrm {[\Omega ]} \\[ 5pt ] \mathrm {j}X_{\mathrm {L10MHz}} &=&\mathrm {j}2\pi f L \\[ 5pt ] &=&\mathrm {j}2\pi \times 10 \times 10^{6} \times \frac {1}{4\pi } \\[ 5pt ] &=&\mathrm {j}5 \times 10^{6} \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ X_{\mathrm {C10MHz}} \ \mathrm {[\Omega ]} \ \)は非常に小さくほぼ短絡状態，\( \ X_{\mathrm {L10MHz}} \ \mathrm {[\Omega ]} \ \)は非常に大きくほぼ開放状態であることが分かる。よって，電流はほぼすべてコンデンサ側に流れることがわかり，\( \ R_{1} \ \)を流れる電流の大きさ\( \ I_{\mathrm {10MHz}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {10MHz}} &=&\frac {V}{R_{1}} \\[ 5pt ] &=&\frac {V}{20} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，求める電流比\( \ \displaystyle \frac {I_{\mathrm {10Hz}}}{I_{\mathrm {10MHz}}} \ \)は，
\[
\begin{eqnarray}
\frac {I_{\mathrm {10Hz}}}{I_{\mathrm {10MHz}}} &=&\frac {\displaystyle \frac {V}{50}}{\displaystyle \frac {V}{20}} \\[ 5pt ] &=&\frac {20}{50} \\[ 5pt ] &=&0.4 \\[ 5pt ] \end{eqnarray}
\] と求められる。