《理論》〈電気回路〉[R05上:問15]Δ結線した三相平衡回路の消費電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図の平衡三相回路について，次の(a)及び(b)に答えよ。

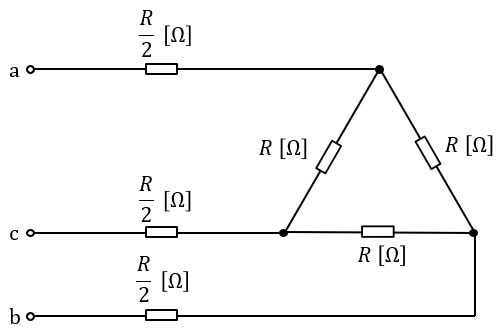
(a)　端子\( \ \mathrm {a} \ \)，\( \ \mathrm {c} \ \)に\( \ 100 \ \mathrm {V} \ \)の単相交流電源を接続したところ、回路の消費電力は\( \ 200 \ \mathrm {W} \ \)であった。抵抗\( \ R \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.30 \ \)　　(2)　\( \ 30 \ \)　　(3)　\( \ 33 \ \)　　(4)　\( \ 50 \ \)　　(5)　\( \ 83 \ \)

(b)　端子\( \ \mathrm {a} \ \)，\( \ \mathrm {b} \ \)，\( \ \mathrm {c} \ \)に線間電圧\( \ 200 \ \mathrm {V} \ \)の対称三相交流電源を接続したときの全消費電力の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.48 \ \)　　(2)　\( \ 0.80 \ \)　　(3)　\( \ 1.2 \ \)　　(4)　\( \ 1.6 \ \)　　(5)　\( \ 4.0 \ \)

【ワンポイント解説】

三相平衡回路における抵抗の消費電力に関する問題です。
\( \ 3 \ \)種では圧倒的に三相平衡回路が出題されやすいので，三相平衡回路の\( \ \Delta – \mathrm {Y} \ \)変換は必ずマスターしておきましょう。
平成22年問15に全く同じ問題が出題されています。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
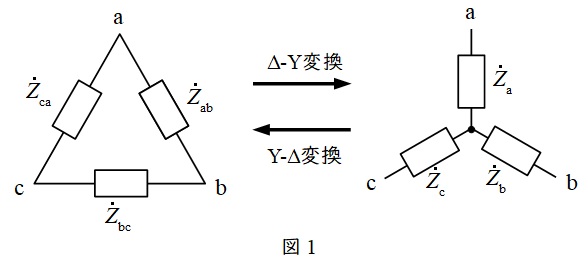
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y}-\Delta \ \)変換
図1において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\] となります。

3.抵抗での消費電力
ある抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)をかけたとき抵抗に電流\( \ I \ \mathrm {[A]} \ \)が流れたとすると，\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] \end{eqnarray}
\] となります。オームの法則\( \ V=RI \ \)より上式は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] と変形できます。

【解答】

(a)解答：(2)
ワンポイント解説「2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り，問題図を\( \ \Delta -\mathrm {Y} \ \)変換すると図2のようになる。
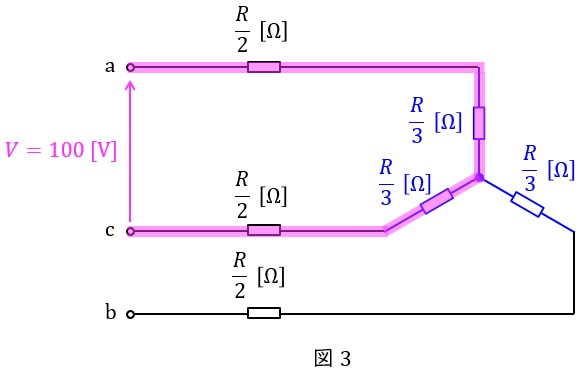
端子\( \ \mathrm {a} \ \)，\( \ \mathrm {c} \ \)に\( \ V=100 \ \mathrm {[V]} \ \)の電源を繋ぐと，電流が流れるのは図3に示した箇所であるため，このときの合成抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{\mathrm {0}}&=&\frac {R}{2}+\frac {R}{3}+\frac {R}{3}+\frac {R}{2} \\[ 5pt ] &=&\frac {5R}{3} \\[ 5pt ] \end{eqnarray}
\] なり，このときに回路で消費される電力が\( \ P=200 \ \mathrm {[W]} \ \)であるから，ワンポイント解説「3.抵抗での消費電力」より，
\[
\begin{eqnarray}
P &=&\frac {V^{2}}{R_{\mathrm {0}}} \\[ 5pt ] R_{\mathrm {0}} &=&\frac {V^{2}}{P} \\[ 5pt ] \frac {5R}{3}&=&\frac {V^{2}}{P} \\[ 5pt ] R&=&\frac {3V^{2}}{5P} \\[ 5pt ] &=&\frac {3\times 100^{2}}{5\times 200} \\[ 5pt ] &=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
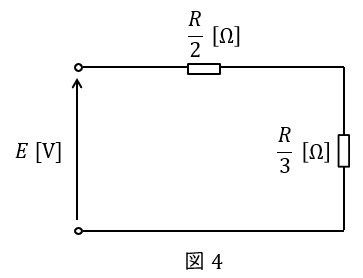
題意に沿って一相分等価回路を描くと図4のようになる。
対称三相交流電源の相電圧は\( \ \displaystyle E=\frac {200}{\sqrt {3}} \ \mathrm {[V]} \ \)であり，一相あたりの抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{\mathrm {1}}&=&\frac {R}{2}+\frac {R}{3} \\[ 5pt ] &=&\frac {5R}{6} \\[ 5pt ] &=&\frac {5\times 30}{6} \\[ 5pt ] &=&25 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるため，全消費電力\( \ P_{3} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{3}&=&3\cdot \frac {E^{2}}{R_{\mathrm {1}}} \\[ 5pt ] &=&3\times \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{25} \\[ 5pt ] &=&1 \ 600 \ \mathrm {[W]}　→　1.6 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。