《理論》〈電子理論〉[H27:問18]演算増幅器に関する計算・空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

演算増幅器(オペアンプ)について，次の(a)及び(b)の問に答えよ。

(a)　演算増幅器は，その二つの入力端子に加えられた信号の$\fbox {　 （ア） 　}$を高い利得で増幅する回路である。演算増幅器の入力インピーダンスは極めて$\fbox {　 （イ） 　}$ため，入力端子電流は$\fbox {　 （ウ） 　}$とみなしてよい。一方，演算増幅器の出力インピーダンスは非常に$\fbox {　 （エ） 　}$ため，その出力端子電圧は負荷による影響を$\fbox {　 （オ） 　}$。さらに，演算増幅器は利得が非常に大きいため，抵抗などの部品を用いて負帰還をかけたときに安定した有限の電圧利得が得られる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
$$\begin{array}{cccccc} & （ア） & （イ） & （ウ） & （エ） & （オ） \\ \hline (1) & 差動成分 & 大きい & ほぼ零 & 小さい & 受けにくい \\ \hline (2) & 差動成分 & 小さい & ほぼ零 & 大きい & 受けやすい \\ \hline (3) & 差動成分 & 大きい & 極めて大きな値 & 大きい & 受けやすい \\ \hline (4) & 同相成分 & 大きい & ほぼ零 & 小さい & 受けやすい \\ \hline (5) & 同相成分 & 小さい & 極めて大きな値 & 大きい & 受けにくい \\ \hline \end{array}$$

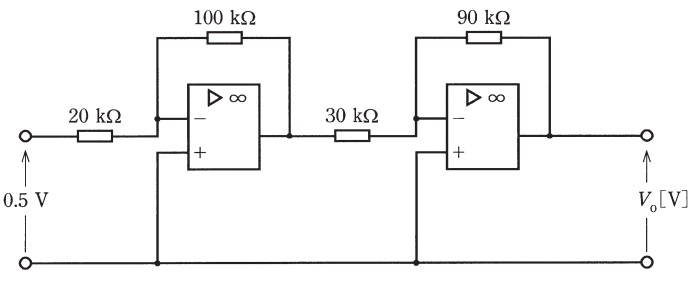
(b)　図のような直流増幅回路がある。この回路に入力電圧$0.5 \ \mathrm {V}$を加えたとき，出力電圧$V_{\mathrm {o}}$の値$\mathrm {[V]}$と電圧利得$A_{\mathrm {V}}$の値$\mathrm {[dB]}$の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

　ただし，演算増幅器は理想的なものとし，$\log _{10}2=0.301，\log _{10}3=0.477$とする。

$$\begin{array}{ccc} & 　　V_{0}　　 & 　　A_{\mathrm {V}}　　 \\[ 5pt ] \hline (1) & 7.5 & 12 \\[ 5pt ] \hline (2) & -15 & 12 \\[ 5pt ] \hline (3) & -7.5 & 24 \\[ 5pt ] \hline (4) & 15 & 24 \\[ 5pt ] \hline (5) & 7.5 & 24 \\[ 5pt ] \hline \end{array}$$

【ワンポイント解説】

この年の選択問題は問17が非常に難しかったため，こちらの問題を選択された方がほとんどではなかったかと思います。オペアンプは計算のパターンが決まっている場合がほとんどなので，出題されたら確実に得点できるようにしましょう。

1.理想的なオペアンプの特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$0\mathrm {V}$(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

2.電圧利得$G_{\mathrm {v}}$
入力電圧$V_{\mathrm {i}}$，出力電圧$V_{\mathrm {o}}$とすると，電圧利得$G_{\mathrm {v}}$は，
$$G_{\mathrm {v}}=20\log _{10}\left| \frac {V_{\mathrm {o}}}{V_{\mathrm {i}}}\right|$$ となります。

【解答】

(a)解答：(1)
ワンポイント解説「1.理想的なオペアンプの特徴」の通りです。

(b)解答：(5)
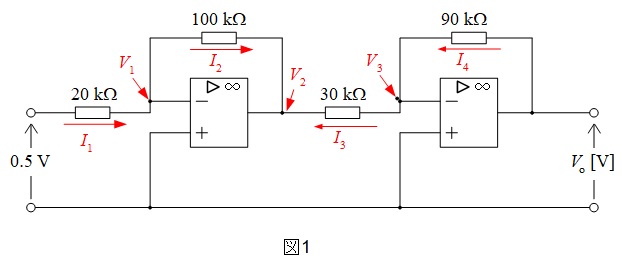
各部の電圧及び電流を図1の通り指定する。
電圧$V_{1}$の大きさは，オペアンプの入力端子間の電圧が$0\mathrm {V}$のため，$V_{1}=0\mathrm {[V]}$となる。
電流$I_{1}$の大きさは，
$$\begin{eqnarray} I_{1}&=&\frac {0.5-0}{20\times 10^{3}} \\[ 5pt ] &=&2.5\times 10 ^{-5} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ となる。
オペアンプの入力端子には電流は流れないので，$I_{1}$はそのまま$100\mathrm {k\Omega }$の抵抗に流れる。したがって，
$$I_{2}=I_{1}=2.5\times 10 ^{-5} \ \mathrm {[A]}$$ となる。
オペアンプの出力電圧$V_{2}$は，
$$\begin{eqnarray} V_{2}&=&V_{1}-100\times 10^{3} I_{2} \\[ 5pt ] &=&0-100\times 10^{3} \times 2.5\times 10 ^{-5} \\[ 5pt ] &=&-2.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ となる。
一方，右側のオペアンプも同様に計算すると，$V_{3}=0\mathrm {[V]}$となるので，
$$\begin{eqnarray} I_{3}&=&\frac {0-(-2.5)}{30\times 10^{3}} \\[ 5pt ] &≒&8.3333\times 10 ^{-5} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}$$ となり，
$$I_{4}=I_{3}=8.3333\times 10 ^{-5} \ \mathrm {[A]}$$ となるので，出力電圧$V_{\mathrm {o}}$は，
$$\begin{eqnarray} V_{\mathrm {o}}&=&90\times 10^{3} I_{4} \\[ 5pt ] &=&90\times 10^{3} \times 8.3333\times 10 ^{-5} \\[ 5pt ] &≒&7.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。
また，ワンポイント解説「2.電圧利得$G_{\mathrm {v}}$」の通り，電圧利得$G_{\mathrm {v}}$は，
$$\begin{eqnarray} G_{\mathrm {v}}&=&20\log _{10}\left| \frac {V_{\mathrm {o}}}{V_{\mathrm {i}}}\right| \\[ 5pt ] &=&20\log _{10}\left| \frac {7.5}{0.5}\right| \\[ 5pt ] &=&20\log _{10}15 \\[ 5pt ] &=&20\log _{10}3 +20\log _{10}5 \\[ 5pt ] &=&20\log _{10}3 +20\log _{10}\frac {10}{2} \\[ 5pt ] &=&20\log _{10}3 +20\log _{10}10-20\log _{10}2 \\[ 5pt ] &=&20(\log _{10}3 +\log _{10}10-\log _{10}2) \\[ 5pt ] &=&20\times (0.477 +1-0.301) \\[ 5pt ] &≒&24 \ \mathrm {[dB]} \\[ 5pt ] \end{eqnarray}$$ と求められる。