Contents
【問題】
【難易度】★★★☆☆(普通)
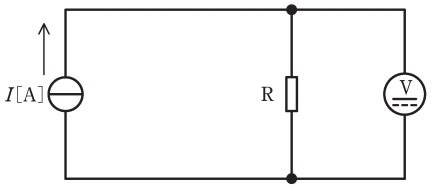
内部抵抗が\( \ 15 \ \mathrm {k\Omega } \ \)の\( \ 150 \ \mathrm {V} \ \)測定端子と内部抵抗が\( \ 10 \ \mathrm {k\Omega } \ \)の\( \ 100 \ \mathrm {V} \ \)測定端子をもつ永久磁石可動コイル形直流電圧計がある。この直流電圧計を使用して,図のように,電流\( \ I \ \mathrm {[A]} \ \)の定電流源で電流を流して抵抗\( \ \mathrm {R} \ \)の両端の電圧を測定した。
測定Ⅰ:\( \ 150 \ \mathrm {V} \ \)測定端子で測定したところ,直流電圧計の指示値は\( \ 101.0 \ \mathrm {V} \ \)であった。
測定Ⅱ:\( \ 100 \ \mathrm {V} \ \)測定端子で測定したところ,直流電圧計の指示値は\( \ 99.00 \ \mathrm {V} \ \)であった。
次の(a)及び(b)の問に答えよ。ただし,測定に用いた機器の指示値に誤差はないものとする。
(a) 抵抗\( \ \mathrm {R} \ \)の抵抗値\( \ [\Omega ] \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 241 \ \) (2) \( \ 303 \ \) (3) \( \ 362 \ \) (4) \( \ 486 \ \) (5) \( \ 632 \ \)
(b) 電流\( \ I \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.08 \ \) (2) \( \ 0.17 \ \) (3) \( \ 0.25 \ \) (4) \( \ 0.36 \ \) (5) \( \ 0.49 \ \)
【ワンポイント解説】
回路方程式自体は普通の直流回路の問題になるのでそれほど難しくないと思いますが,計算がやや複雑な問題と言えます。電験の理論科目は時間と戦いでもあります。日常の学習から電卓での計算(メモリー機能が扱えると理想です。)を早くできるようにしましょう。
1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが,法則を説明できる必要はなく,計算で使いこなせることが重要です。
①第1法則(電流則)
回路の接続点に流入する電流の和と流出する電流の和が等しい。
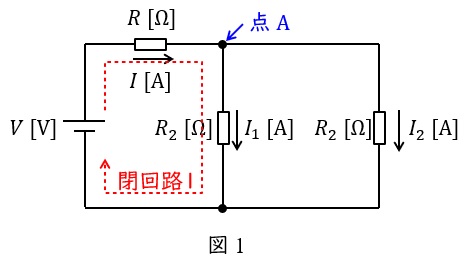
図1で言えば,例えば接続点\( \ \mathrm {A} \ \)において,
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②第2法則(電圧則)
任意の閉回路において,起電力の総和と抵抗の電圧降下の和は等しい。
図1で言えば,例えば閉回路\( \ 1 \ \)において,
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(5)
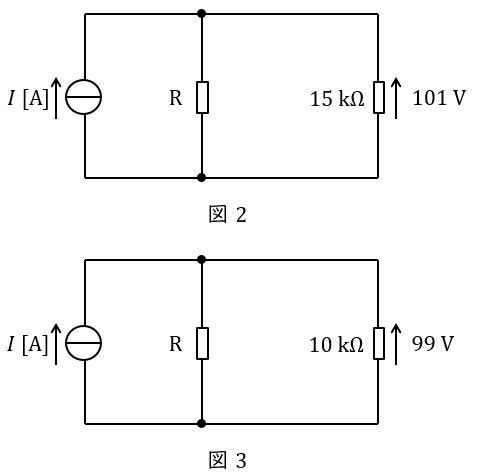
題意に沿って回路を描くと,図2及び図3のようになる。
図2において,並列回路であるから,抵抗\( \ \mathrm {R} \ \)に加わる電圧も\( \ 101.0 \ \mathrm {[V]} \ \)なので,抵抗\( \ \mathrm {R} \ \)の接続点にキルヒホッフの法則の電流則を適用すると,ワンポイント解説「1.キルヒホッフの法則」の通り,
\[
\begin{eqnarray}
\frac {101}{\mathrm {R}}+\frac {101}{15\times 10^{3}} &=&I ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となり,図3においても同様に考えると,
\[
\begin{eqnarray}
\frac {99}{\mathrm {R}}+\frac {99}{10\times 10^{3}} &=&I \ \ ・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。①,②について\( \ I \ \)を消去して整理すると,
\[
\begin{eqnarray}
\frac {101}{\mathrm {R}}+\frac {101}{15\times 10^{3}} &=&\frac {99}{\mathrm {R}}+\frac {99}{10\times 10^{3}} \\[ 5pt ]
\frac {101}{\mathrm {R}}-\frac {99}{\mathrm {R}} &=&\frac {99}{10\times 10^{3}}-\frac {101}{15\times 10^{3}} \\[ 5pt ]
\frac {2}{\mathrm {R}} &=&\left( \frac {99}{10}-\frac {101}{15} \right) \times \frac {1}{10^{3}} \\[ 5pt ]
&=&\frac {297-202}{30} \times \frac {1}{10^{3}} \\[ 5pt ]
&=&\frac {19}{6} \times \frac {1}{10^{3}} \\[ 5pt ]
\mathrm {R}&=&\frac {2\times 6}{19} \times 10^{3} \\[ 5pt ]
&≒&631.6 → 632 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(2)
(1)の解答を①に代入すると,
\[
\begin{eqnarray}
I&=&\frac {101}{\mathrm {R}}+\frac {101}{15\times 10^{3}} \\[ 5pt ]
&=&\frac {101}{631.6}+\frac {101}{15\times 10^{3}} \\[ 5pt ]
&≒&0.167 → 0.17 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは