《理論》〈電気及び電子計測〉[R06上:問16]並列接続した直流電流計の測定可能な電流値に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

直流電流の測定範囲の拡大について，次の(a)及び(b)の問に答えよ。

(a)　直流電流計Ⅰの最大目盛は\( \ 100 \ \mathrm {A} \ \)，直流電流計Ⅱの最大目盛は\( \ 50 \ \mathrm {A} \ \)，直流電流計Ⅲの最大目盛は\( \ 50 \ \mathrm {A} \ \)である。この\( \ 3 \ \)台の直流電流計を並列に接続し，ある回路に接続したところ，直流電流計Ⅰの指示値は\( \ 90 \ \mathrm {A} \ \)，直流電流計Ⅱの指示値は\( \ 40 \ \mathrm {A} \ \)，直流電流計Ⅲの指示値は\( \ 35 \ \mathrm {A} \ \)であった。この接続において計測できる最大電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 100 \ \)　　(2)　\( \ 144 \ \)　　(3)　\( \ 165 \ \)　　(4)　\( \ 183 \ \)　　(5)　\( \ 200 \ \)

(b)　次に，直流電流計Ⅰ，直流電流計Ⅱ，直流電流計Ⅲの\( \ 3 \ \)台を並列に接続した状態で，別の回路に接続した。この回路を流れる電流の値は\( \ 150 \ \mathrm {A} \ \)であった。このとき，各電流計が指示した値は，直流電流計Ⅰ\( = \ \fbox {　 （ア） 　} \ \mathrm {A} \ \)，直流電流計Ⅱ\( = \ \fbox {　 （イ） 　} \ \mathrm {A} \ \)，直流電流計Ⅲ\( = \ \fbox {　 （ウ） 　} \ \mathrm {A} \ \)であった。

上記の記述中の空白箇所(ア)～(ウ)に当てはまる最も近い数値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　31.8　 & 　36.4　 & 　81.8　 \\
\hline
(2) & 　31.8　 & 　81.8　 & 　36.4　 \\
\hline
(3) & 　36.4　 & 　31.8　 & 　81.8　 \\
\hline
(4) & 　81.8　 & 　31.8　 & 　36.4　 \\
\hline
(5) & 　81.8　 & 　36.4　 & 　31.8　 \\
\hline
\end{array}
\]

【ワンポイント解説】

並列接続した直流電流計の測定可能な電流値と各電流計の測定値に関する問題です。
電流比のみを考え特別難解な公式を使用しないので，非常に易しいと感じる受験生と解法に迷う受験生に分かれそうな問題です。
類題が令和4年下期問16に出題されていますので，合わせて学習することをお勧めします。

【解答】

(a)解答：(4)
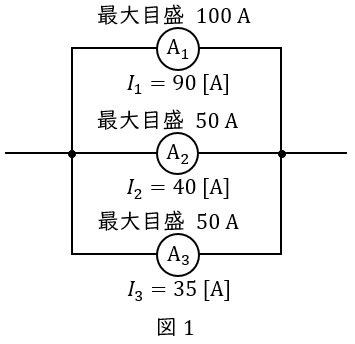
題意に沿って図を描くと図1のようになる。図1より電流比は，
\[
\begin{eqnarray}
I_{1}:I_{2}:I_{3}&=&90:40:35 \\[ 5pt ] &=&18:8:7 \\[ 5pt ] \end{eqnarray}
\] となる。これより，直流電流計Ⅰが最大目盛\( \ 100 \ \mathrm {A} \ \)になるとき，直流電流計Ⅱ及びⅢの電流値\( \ I_{2} \ \mathrm {[A]} \ \)及び\( \ I_{3} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {8}{18}\times I_{1} \\[ 5pt ] &=&\frac {8}{18}\times 100 \\[ 5pt ] &≒&44.44 \ \mathrm {[A]} \\[ 5pt ] I_{3}&=&\frac {7}{18}\times I_{1} \\[ 5pt ] &=&\frac {7}{18}\times 100 \\[ 5pt ] &≒&38.89 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，直流電流計Ⅱが最大目盛\( \ 50 \ \mathrm {A} \ \)になるときの，直流電流計Ⅰの電流値\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {18}{8}\times I_{2} \\[ 5pt ] &=&\frac {18}{8}\times 50 \\[ 5pt ] &=&112.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，最大目盛を超過してしまうため，最大目盛となるのは直流電流計Ⅰである。（直流電流計Ⅲの値はⅡを必ず下回るため最大目盛とならない。）

以上から，計測できる最大電流\( \ I_{\mathrm {m}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {m}}&=&I_{1}+I_{2}+I_{3} \\[ 5pt ] &=&100+44.44+38.89 \\[ 5pt ] &≒&183 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
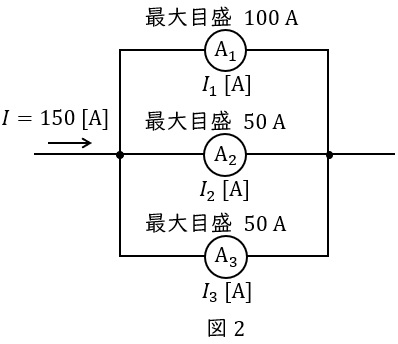
(a)より，流れる電流の比は\( \ I_{1}:I_{2}:I_{3}=18:8:7 \ \)であるから，図2に示すように回路に流れる電流\( \ I=150 \ \mathrm {[A]} \ \)の時の各電流計に流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)，\( \ I_{2} \ \mathrm {[A]} \ \)及び\( \ I_{3} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {18}{18+8+7}\times I \\[ 5pt ] &=&\frac {18}{33}\times 150 \\[ 5pt ] &≒&81.8 \ \mathrm {[A]} \\[ 5pt ] I_{2}&=&\frac {8}{18+8+7}\times I \\[ 5pt ] &=&\frac {8}{33}\times 150 \\[ 5pt ] &≒&36.4 \ \mathrm {[A]} \\[ 5pt ] I_{3}&=&\frac {7}{18+8+7}\times I \\[ 5pt ] &=&\frac {7}{33}\times 150 \\[ 5pt ] &≒&31.8 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。