《理論》〈電磁気〉[R06下:問1]２種類の誘電体を挿入したコンデンサに蓄えられる電荷に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

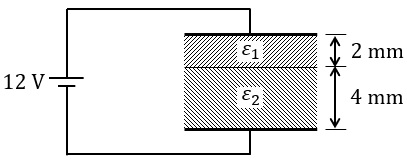
図のように，電極面積\( \ 0.1 \ \mathrm {m^{2}} \ \)，電極間隔\( \ 6 \ \mathrm {mm} \ \)の平行平板コンデンサに，比誘電率\( \ \varepsilon _{1}=2 \ \)，厚さ\( \ 2 \ \mathrm {mm} \ \)及び比誘電率\( \ \varepsilon _{2}=4 \ \)，厚さ\( \ 4 \ \mathrm {mm} \ \)の\( \ 2 \ \)種類の誘電体が電極と平行に挿入されている。このコンデンサに\( \ 12 \ \mathrm {V} \ \)の直流電圧を印加したとき，蓄えられる電荷の値\( \ \mathrm {[C]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，真空の誘電率\( \ \varepsilon _{0}=8.85\times 10^{-12} \ \mathrm {F/m} \ \)とし，コンデンサの端効果は無視するものとする。

　(1)　\( \ 5.3\times 10^{-9} \ \)　　(2)　\( \ 7.8\times 10^{-9} \ \)　　(3)　\( \ 9.4\times 10^{-9} \ \)　
　(4)　\( \ 2.1\times 10^{-8} \ \)　　(5)　\( \ 4.5\times 10^{-8} \ \)

【ワンポイント解説】

誘電率の異なる誘電体を組み合わせ作成したコンデンサに蓄えられる電荷を求める問題です。
直列接続のコンデンサの静電容量なので少し計算量が多くなりそうですが，電験の場合は比較的数値が調整されている場合も多いです。最初から計算量が多いと決めつけず，まずは求められるところを一つずつ求めていくようにして下さい。
本問はやや古いですが，平成7年問1からの再出題となります。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)，極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \)，極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると，
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)の合成静電容量\( \ C \ \mathrm {[F]} \ \)は，
　　並列接続時：\( \ C=C_{1}+C_{2} \ \)
　　直列接続時：\( \ \displaystyle C=\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ \)
となります。

【解答】

解答：(1)
比誘電率\( \ \varepsilon _{\mathrm {1}}=2 \ \)の誘電体部の静電容量\( \ C_{1} \ \mathrm {[F]} \ \)及び比誘電率\( \ \varepsilon _{\mathrm {2}}=4 \ \)の誘電体部の静電容量\( \ C_{2} \ \mathrm {[F]} \ \)は，ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り，
\[
\begin{eqnarray}
C_{1} &=&\frac {\varepsilon _{\mathrm {1}}\varepsilon _{0}S}{d_{1}} \\[ 5pt ] &=&\frac {2\times 8.85\times 10^{-12}\times 0.1}{2\times 10^{-3}} \\[ 5pt ] &=&8.85\times 10^{-10} \ \mathrm {[F]} \\[ 5pt ] C_{2} &=&\frac {\varepsilon _{\mathrm {2}}\varepsilon _{0}S}{d_{2}} \\[ 5pt ] &=&\frac {4\times 8.85\times 10^{-12}\times 0.1}{4\times 10^{-3}} \\[ 5pt ] &=&8.85\times 10^{-10} \ \mathrm {[F]}=C_{1} \\[ 5pt ] \end{eqnarray}
\] となるので，コンデンサ全体の静電容量\( \ C \ \mathrm {[F]} \ \)は，ワンポイント解説「3.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C &=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] &=&\frac {C_{1}^{2}}{C_{1}+C_{1}} \\[ 5pt ] &=&\frac {C_{1}}{2} \\[ 5pt ] &=&\frac {8.85\times 10^{-10}}{2} \\[ 5pt ] &=&4.425\times 10^{-10} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，コンデンサに\( \ V=12 \ \mathrm {[V]} \ \)の直流電圧を印加したとき蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] &=&4.425\times 10^{-10}\times 12 \\[ 5pt ] &=&5.31\times 10^{-9} \ \mathrm {[C]} \\[ 5pt ] \end{eqnarray}
\] と求められる。