《理論》〈電気回路〉[H30:問8]交流回路の位相差の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，角周波数\(\ \omega \ \mathrm {[rad ／ s]}\)の交流電源と力率\(\displaystyle \frac {1}{\sqrt {2}}\)の誘導性負荷\( \ \dot Z \mathrm {[\Omega ]} \ \)との間に，抵抗値\( \ R \mathrm {[\Omega ]} \ \)の抵抗器とインダクタンス\( \ L \mathrm {[H]} \ \)のコイルが接続されている。\(R=\omega L \ \)とするとき，電源電圧\( \ {\dot V}_{1} \mathrm {[V]} \ \)と負荷の端子電圧\( \ {\dot V}_{2} \mathrm {[V]} \ \)との位相差の値\([°]\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

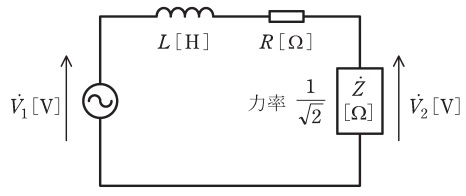
　(1)　\(0\)　　(2)　\(30\)　　(3)　\(45\)　　(4)　\(60\)　　(5)　\(90\)

【ワンポイント解説】

ベクトル図を描けることができるかどうかを問う問題となります。電圧と電流のベクトルは交流回路特有の内容となります。非常に重要な内容となりますので，よく理解しておくようにしましょう。

1.各負荷による電圧と電流のベクトルの関係
交流回路では負荷により電流が進み電流になったり，遅れ電流になったりといった特徴があります。

①抵抗の場合
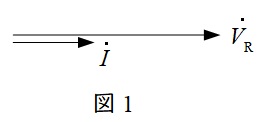
抵抗の場合は電圧と電流の位相は等しくなり，ベクトル図は図1のように描けます。

②インダクタンス（リアクトル）の場合
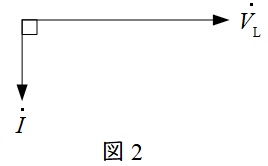
電流が電圧に対して\(90°\)遅れ，ベクトル図は図2のようになります。

③コンデンサの場合
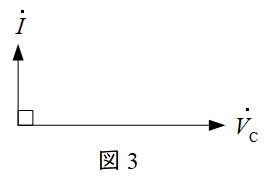
電流が電圧に対して\(90°\)進み，ベクトル図は図3のようになります。

【解答】

解答：(1)
問題図より回路は直列回路であるため，回路に流れる電流\(\dot I\)を基準にベクトル図を作成する。
ワンポイント解説「1.各負荷による電圧と電流のベクトルの関係」より，インダクタンスの電圧\(\mathrm {j}\omega LI\)は電流\(I\)より位相が\(90°\)進み，抵抗の電圧\(RI\)は位相が電流\(I\)と等しくなる。
また，誘導性負荷\(\dot Z\)は力率\(\displaystyle \cos \theta = \frac {1}{\sqrt {2}}\)なので，\(\theta =45°\)となり，電圧\({\dot V}_{2}\)は電流より\(45°\)進むことになる。
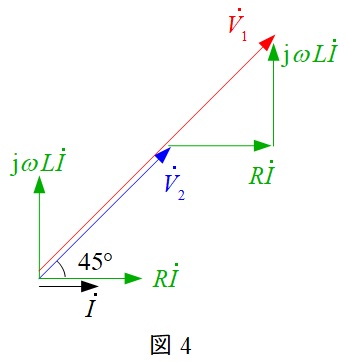
以上の内容をベクトル図に描くと図4のようになる。\({\dot V}_{1}=\mathrm {j}\omega LI +RI +{\dot V}_{2}\)の関係があり，\(R=\omega L\)であるので，\({\dot V}_{1}\)と\({\dot V}_{2}\)の位相は図4の通り等しくなる。
よって，\( \ {\dot V}_{1} \ \)と\( \ {\dot V}_{2} \ \)の位相差は\(0°\)と求められる。