《理論》〈電気回路〉[R01:問5]直流回路の電位計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

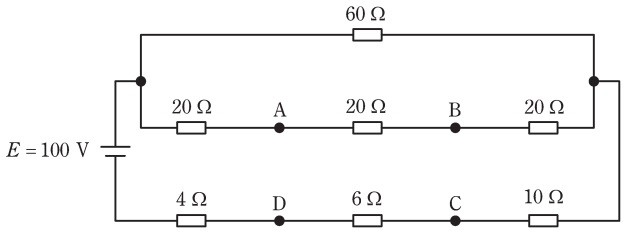
図のように，七つの抵抗及び電圧\( \ E=100 \ \mathrm {V} \ \)の直流電源からなる回路がある。この回路において，\( \ \mathrm {A－D} \ \)間，\( \ \mathrm {B－C} \ \)間の各電位差を測定した。このとき，\( \ \mathrm {A－D} \ \)間の電位差の大きさ\( \ \mathrm {[V]} \ \)及び\( \ \mathrm {B－C} \ \)間の電位差の大きさ\( \ \mathrm {[V]} \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& 　　\ \mathrm {A－D} \ 間の電位差の大きさ　　 & 　　\ \mathrm {B－C} \ 間の電位差の大きさ　　 \\
\hline
(1) & 28 & 60 \\
\hline
(2) & 40 & 72 \\
\hline
(3) & 60 & 28 \\
\hline
(4) & 68 & 80 \\
\hline
(5) & 72 & 40 \\
\hline
\end{array}
\]

【ワンポイント解説】

計算はやや面倒ですが，電流の流れから感覚的に\( \ \mathrm {A－D} \ \)間の電位差の方が\( \ \mathrm {B－C} \ \)間の電位差より大きいことにピンと来ると良いと思います。それだけでこの問題は五択から二択に変わります。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
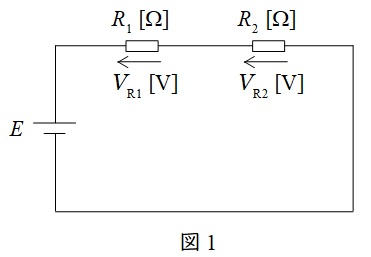
図1に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

②分流の法則
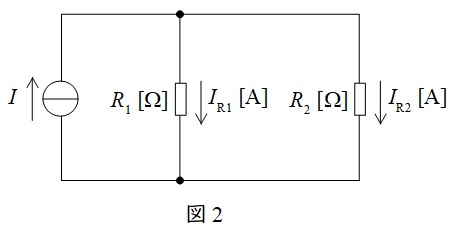
図2に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(5)
図3のように各部の直列合成抵抗を\( \ R_{1} \ \)，\( \ R_{2} \ \)とおくと，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{1}&=&20+20+20 \\[ 5pt ] &=&60 \ \mathrm {[\Omega ]} \\[ 5pt ] R_{2}&=&4+6+10 \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，図4のように書き換えることができる。

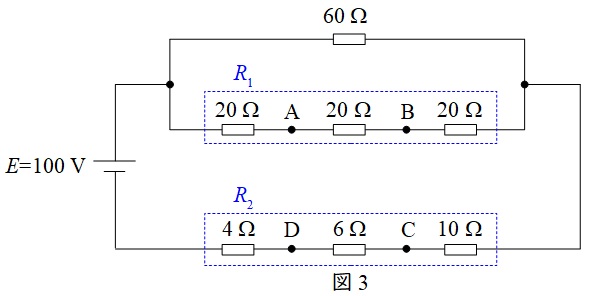
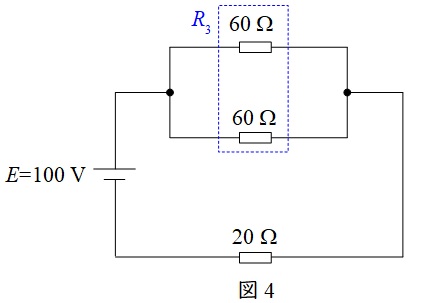
図4のように，\( \ 60 \ \mathrm {\Omega } \ \)同士の並列合成抵抗を\( \ R_{3} \ \)とおくと，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{3}&=&\frac {60\times 60}{60+60} \\[ 5pt ] &=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，図5のように書き換えることができる。

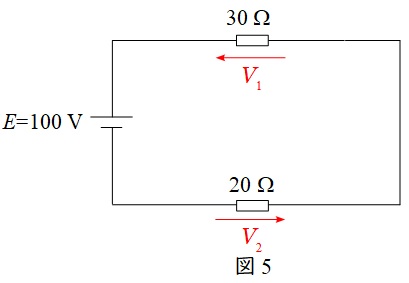
図5において，\( \ 30 \ \mathrm {\Omega } \ \)にかかる電圧を\( \ V_{1} \ \)，\( \ 20 \ \mathrm {\Omega } \ \)にかかる電圧を\( \ V_{2} \ \)とおくと，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
V_{1}&=&\frac {30}{30+20}\times E \\[ 5pt ] &=&\frac {30}{30+20}\times 100 \\[ 5pt ] &=&60 \ \mathrm {[V]} \\[ 5pt ] V_{2}&=&\frac {20}{30+20}\times E \\[ 5pt ] &=&\frac {20}{30+20}\times 100 \\[ 5pt ] &=&40 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。それぞれの電圧を問題図に当てはめると図6のようになる。

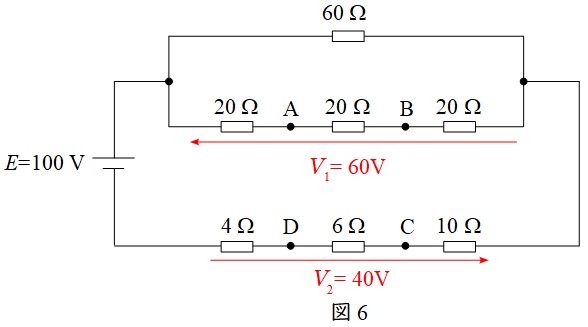
図6より，\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)，\( \ \mathrm {C} \ \)，\( \ \mathrm {D} \ \)それぞれの電位\( \ V_{\mathrm {A}} \ \)，\( \ V_{\mathrm {B}} \ \)，\( \ V_{\mathrm {C}} \ \)，\( \ V_{\mathrm {D}} \ \)は，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&\frac {20+20}{20+20+20}V_{1}+V_{2} \\[ 5pt ] &=&\frac {20+20}{20+20+20}\times 60+40 \\[ 5pt ] &=&80 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {B}}&=&\frac {20}{20+20+20}V_{1}+V_{2} \\[ 5pt ] &=&\frac {20}{20+20+20}\times 60+40 \\[ 5pt ] &=&60 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {C}}&=&\frac {4+6}{4+6+10}V_{2} \\[ 5pt ] &=&\frac {4+6}{4+6+10}\times 40 \\[ 5pt ] &=&20 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {D}}&=&\frac {4}{4+6+10}V_{2} \\[ 5pt ] &=&\frac {4}{4+6+10}\times 40 \\[ 5pt ] &=&8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {A－D} \ \)間，\( \ \mathrm {B－C} \ \)間の角電位差\( \ V_{\mathrm {AD}} \ \)及び\( \ V_{\mathrm {BC}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {AD}}&=&V_{\mathrm {A}}-V_{\mathrm {D}} \\[ 5pt ] &=&80-8 \\[ 5pt ] &=&72 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {BC}}&=&V_{\mathrm {B}}-V_{\mathrm {C}} \\[ 5pt ] &=&60-20 \\[ 5pt ] &=&40 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。