平成30年理論(問4)の考え方について教えて下さい。

【質問】

電験3種平成30年理論の問4の問題なんですが、\( \ \Delta H_{\mathrm {x}} \ \)を求める時の\( \ \displaystyle \frac {a}{\sqrt {a^{2}+x^{2}}} \ \)はどこから導きだした\( \ \sin \theta \ \)なのでしょうか？
宜しくお願いします。

【回答】

ご質問ありがとうございます。
数学的な説明が不十分であり，申し訳ありません。こちらで補足させて頂きます。
\( \ \displaystyle \frac {a}{\sqrt {a^{2}+x^{2}}} \ \)は\( \ \sin \theta \ \)ではありません。
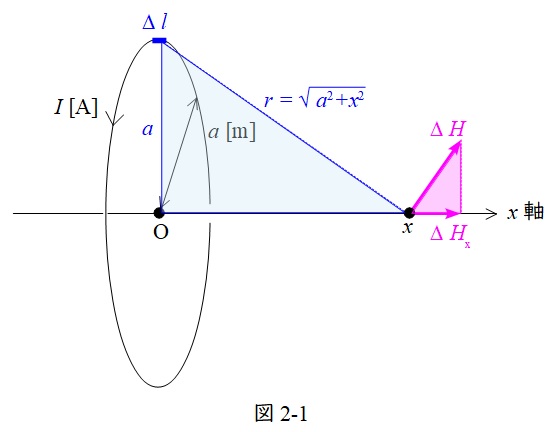
図2-1のように，問題解答の図2でできる青の直角三角形と赤の直角三角形の二つの三角形について考えます。
左の青の三角形では一番長い辺が\( \ r=\sqrt {a^{2}+x^{2}} \ \)となっており，縦の一番短い辺の長さが\( \ a \ \)となります。
一方，右の赤の三角形では一番長い辺が\( \ \Delta H \ \)，一番短い辺の長さが\( \ \Delta H_{\mathrm {x}} \ \)となります。
それぞれの三角形の角度の関係を見ればわかりますが，この二つの三角形は相似な三角形となっていますので，
\[
\begin{eqnarray}
\frac {a}{r}&=&\frac {\Delta H_{\mathrm {x}}}{\Delta H} \\[ 5pt ] \frac {a}{\sqrt {a^{2}+x^{2}}}&=&\frac {\Delta H_{\mathrm {x}}}{\Delta H} \\[ 5pt ] \end{eqnarray}
\] という関係が成立します。これを\( \ \Delta H_{\mathrm {x}} \ \)について解くと，
\[
\begin{eqnarray}
\frac {\Delta H_{\mathrm {x}}}{\Delta H}&=&\frac {a}{\sqrt {a^{2}+x^{2}}} \\[ 5pt ] \Delta H_{\mathrm {x}}&=&\Delta H\cdot \frac {a}{\sqrt {a^{2}+x^{2}}} \\[ 5pt ] \end{eqnarray}
\] の関係が導かれます。

※質問者様
　ご連絡頂きましたメールアドレスに送付したところ，エラーにて返信することができませんでした。このページを以て回答とさせて頂きます。