Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
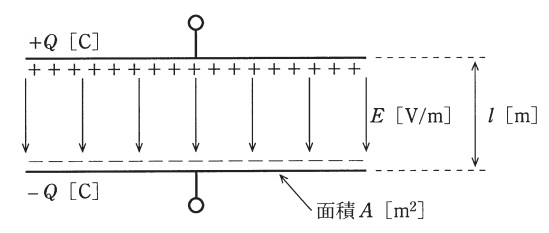
図のように,真空中で2枚の電極を平行に向かい合せたコンデンサを考える。各電極の面積を\(A \ \mathrm {[m^{2}]}\),電極の間隔を\(l \ \mathrm {[m]}\)とし,端効果は無視すると,静電容量は\(\fbox { (ア) } \ \mathrm {[F]}\)である。このコンデンサに直流電圧源を接続し,電荷\(Q \ \mathrm {[C]}\)を充電してから電圧源を外した。このとき,電極間の電界\(E=\fbox { (イ) } \ \mathrm {[V/m]}\)によって静電エネルギー\(W=\fbox { (ウ) } \ \mathrm {[J]}\)が蓄えられている。この状態で電極間隔を増大させると静電エネルギーも増大することから,二つの電極間には静電力の\(\fbox { (エ) }\)が働くことが分かる。
ただし,真空の誘電率を\(\varepsilon _{0} \ \mathrm {[F/m]}\)とする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & \displaystyle \varepsilon _{0}\frac {A}{l} & \displaystyle \frac {Ql}{\varepsilon _{0}A} & \displaystyle \frac {Q^{2}l}{\varepsilon _{0}A} & 引 力 \\
\hline
(2) & \displaystyle \varepsilon _{0}\frac {A}{l} & \displaystyle \frac {Q}{\varepsilon _{0}A} & \displaystyle \frac {Q^{2}l}{2\varepsilon _{0}A} & 引 力 \\
\hline
(3) & \displaystyle \frac {A}{\varepsilon _{0}l} & \displaystyle \frac {Ql}{\varepsilon _{0}A} & \displaystyle \frac {Q^{2}l}{2\varepsilon _{0}A} & 斥 力 \\
\hline
(4) & \displaystyle \frac {A}{\varepsilon _{0}l} & \displaystyle \frac {Q}{\varepsilon _{0}A} & \displaystyle \frac {Q^{2}l}{\varepsilon _{0}A} & 斥 力 \\
\hline
(5) & \displaystyle \varepsilon _{0}\frac {A}{l} & \displaystyle \frac {Q}{\varepsilon _{0}A} & \displaystyle \frac {Q^{2}l}{2\varepsilon _{0}A} & 斥 力 \\
\hline
\end{array}
\]
【ワンポイント解説】
問1と同様に基本公式を理解しているかどうかが重要になります。電極間に引力が働くことは基本として理解しておきましょう。
1.平行平板コンデンサの電荷\(Q\)と静電容量\(C\),電圧\(V\)の関係
静電容量\(C\)の平行平板コンデンサに電圧\(V\)をかけ,十分時間が経った時に蓄えられる電荷\(Q\)は,
\[
Q=CV
\]
となります。
2.平行平板コンデンサの静電容量\(C\)の導出
平行平板コンデンサの極板の面積を\(S\),極板間の距離を\(d\),極板間の誘電率を\(\varepsilon \)とすると平行平板コンデンサの静電容量\(C\)は,
\[
C=\frac {\varepsilon S}{d}
\]
となります。
3.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係
極板間の距離\(d\)の平行平板コンデンサに電圧\(V\)をかけると,極板間の電界\(E\)は,
\[
E=\frac {V}{d}
\]
となります。
4.コンデンサ間に蓄えられるエネルギー\(W\)
極板間の距離\(d\)の平行平板コンデンサに電圧\(V\)をかけると,極板間に蓄えられるエネルギー\(W\)は,
\[
W=\frac {1}{2}CV^{2}
\]
となります。また,\(Q=CV\)の関係から,
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ]
&=&\frac {1}{2}QV \\[ 5pt ]
&=&\frac {Q^{2}}{2C}
\end{eqnarray}
\]
となります。
【解答】
解答:(2)
(ア)
ワンポイント解説「2.平行平板コンデンサの静電容量\(C\)の導出」より,
\[
C=\varepsilon _{0} \frac {A}{l}
\]
と求められる。
(イ)
ワンポイント解説「3.平行平板コンデンサの電界\(E\)と電圧\(V\)の関係」より,
\[
\begin{eqnarray}
E &=&\frac {V}{l} \\[ 5pt ]
&=&\frac {Q}{Cl} \\[ 5pt ]
&=&\frac {Ql}{\varepsilon _{0}Al} \\[ 5pt ]
&=&\frac {Q}{\varepsilon _{0}A}
\end{eqnarray}
\]
と求められる。
(ウ)
ワンポイント解説「4.コンデンサ間に蓄えられるエネルギー\(W\)」より,
\[
\begin{eqnarray}
W &=&\frac {Q^{2}}{2C} \\[ 5pt ]
&=&\frac {Q^{2}l}{2\varepsilon _{0}A}
\end{eqnarray}
\]
と求められる。
(エ)
(ウ)の解答式より,\(W\)は\(l\)に比例して増大する。\(W=F\Delta l\)の関係より,力\(F\)に逆らって\(\Delta l\)動かすとエネルギーが増大することになるので,\(F\)は引力となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは