《電力》〈配電〉[H23:問9]単相3線式配電線路における電圧及び電流の値に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

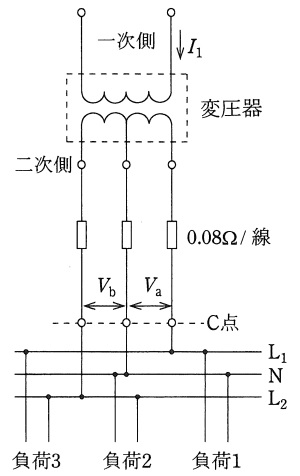
一次電圧\( \ 6 \ 400 \ \mathrm {[V]} \ \)，二次電圧\( \ 210 \ \mathrm {[V]} / 105 \ \mathrm {[V]} \ \)の柱上変圧器がある。図のような単相\( \ 3 \ \)線式配電線路において三つの無誘導負荷が接続されている。負荷\( \ 1 \ \)の電流は\( \ 50 \ \mathrm {[A]} \ \)，負荷\( \ 2 \ \)の電流は\( \ 60 \ \mathrm {[A]} \ \)，負荷\( \ 3 \ \)の電流は\( \ 40 \ \mathrm {[A]} \ \)である。\( \ \mathrm {L}_{\mathrm {1}} \ \)と\( \ \mathrm {N} \ \)間の電圧\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)，\( \ \mathrm {L}_{\mathrm {2}} \ \)と\( \ \mathrm {N} \ \)間の電圧\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)，及び変圧器一次電流\( \ I_{\mathrm {1}} \ \mathrm {[A]} \ \)の値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，変圧器から低圧負荷までの電線\( \ 1 \ \)線当たりの抵抗を\( \ 0.08 \ \mathrm {[\Omega ]} \ \)とし，変圧器の励磁電流，インピーダンス，低圧配電線のリアクタンス，及び\( \ \mathrm {C} \ \)点から負荷側線路のインピーダンスは考えないものとする。

\[
\begin{array}{cccc}
& V_{\mathrm {a}} \ \mathrm {[V]} & V_{\mathrm {b}} \ \mathrm {[V]} & I_{\mathrm {1}} \ \mathrm {[A]} \\
\hline
(1) & 　98.6　 & 　96.2　 & 　3.12　 \\
\hline
(2) & 　97.0　 & 　97.8　 & 　3.28　 \\
\hline
(3) & 　97.0　 & 　97.8　 & 　2.95　 \\
\hline
(4) & 　96.2　 & 　98.6　 & 　3.12　 \\
\hline
(5) & 　98.6　 & 　96.2　 & 　3.28　 \\
\hline
\end{array}
\]

【ワンポイント解説】

単相\( \ 3 \ \)線式配電線路の線路計算に関する問題です。
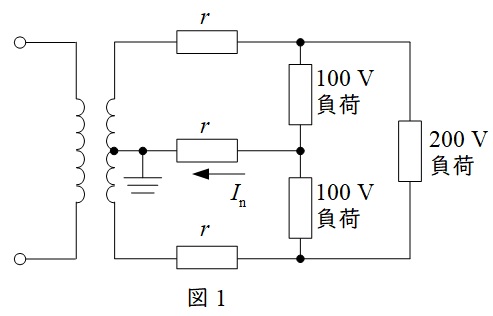
問題図でそのまま計算するとわかりにくいので，図1に示すような一般的な回路に書き換えると解きやすいと思います。

1.単相\( \ 3 \ \)線式配電方式
単相\( \ 3 \ \)線式配電方式は図1のような回路で低圧の需要家に配電する方式で以下のような特徴があります。
・\( \ 100 \ \mathrm {[V]} \ \)負荷と\( \ 200 \ \mathrm {[V]} \ \)負荷の双方に供給可能
・線路負荷が平衡している時，中性点電流\( \ I_{\mathrm {n}} \ \)は零となる
・線路負荷が平衡しており，線間電圧，線電流が等しい場合，単相\( \ 2 \ \)線式に比べ線路電流は\( \ \displaystyle \frac {1}{2} \ \)となるので，線路損失は\( \ \displaystyle \frac {1}{4} \ \)となる

2.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，それぞれの関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
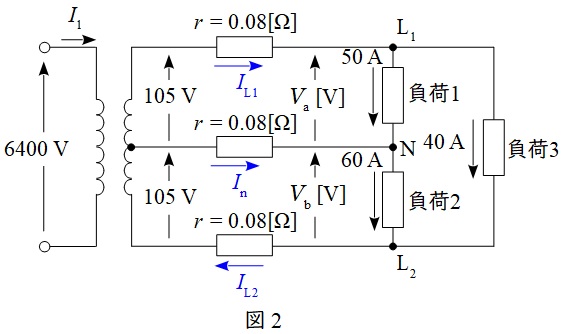
問題図を一般的な単相\( \ 3 \ \)線式の回路に書き換えると図2のようになる。
図2において，電圧線\( \ \mathrm {L}_{1} \ \)を流れる電流\( \ I_{\mathrm {L1}} \ \mathrm {[A]} \ \)，電圧線\( \ \mathrm {L}_{2} \ \)を流れる電流\( \ I_{\mathrm {L2}} \ \mathrm {[A]} \ \)，中性線\( \ \mathrm {N} \ \)を流れる電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {L1}} &=&50+40 \\[ 5pt ] &=&90 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {L2}} &=&60+40 \\[ 5pt ] &=&100 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {n}} &=&60-50 \\[ 5pt ] &=&10 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから，電圧線\( \ \mathrm {L}_{1} \ \)の電位\( \ V_{\mathrm {L1}} \ \mathrm {[V]} \ \)，電圧線\( \ \mathrm {L}_{2} \ \)の電位\( \ V_{\mathrm {L2}} \ \mathrm {[V]} \ \)，中性線\( \ \mathrm {N} \ \)の電位\( \ V_{\mathrm {N}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {L1}} &=&105-rI_{\mathrm {L1}} \\[ 5pt ] &=&105-0.08\times 90 \\[ 5pt ] &=&97.8 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {N}} &=&0-rI_{\mathrm {n}} \\[ 5pt ] &=&0-0.08\times 10 \\[ 5pt ] &=&-0.8 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {L2}} &=&-105+rI_{\mathrm {L2}} \\[ 5pt ] &=&-105+0.08\times 100 \\[ 5pt ] &=&-97 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ \mathrm {L}_{\mathrm {1}} \ \)と\( \ \mathrm {N} \ \)間の電圧\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)，\( \ \mathrm {L}_{\mathrm {2}} \ \)と\( \ \mathrm {N} \ \)間の電圧\( \ V_{\mathrm {b}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {a}} &=&V_{\mathrm {L1}}-V_{\mathrm {N}} \\[ 5pt ] &=&97.8-\left( -0.8\right) \\[ 5pt ] &=&98.6 \ \mathrm {[V]} \\[ 5pt ] V_{\mathrm {b}} &=&V_{\mathrm {N}}-V_{\mathrm {L2}} \\[ 5pt ] &=&-0.8-\left( -97\right) \\[ 5pt ] &=&96.2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，変圧器における一次と二次の電力の大きさは等しいので，
\[
\begin{eqnarray}
V_{1}I_{1} &=&V_{2}I_{\mathrm {L1}}+V_{2}I_{\mathrm {L2}} \\[ 5pt ] 6400\times I_{1} &=&105 \times 90+105\times 100 \\[ 5pt ] I_{1}&≒&3.12 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。